通用回归神经网络在声呐目标分类中的应用
通用回归神经网络在声呐目标分类中的应用
BURCU ERKMEN TULAY YILDMM
摘要:应用有源声呐在浅水区水下水雷的远距离探测从而维护重要海港和海岸线区域的安全性是必需、重要的科目。人类专家从事的从海底上的水雷和岩石反馈有源声呐进行的工作通常是十分困难而且工作量非常庞大。由于它的自适应和并行处理能力,神经网络分类器已经被广泛应用在复杂声呐信号的分类中。此文,通用回归神经网络应用于解决水下目标分类的问题,作为特征抽取的主元分析已经被建立起来提高分类性能。接受器工作特性分析在神经分类器上用来评估诊断程序的灵敏度和比功率上得以应用.
1. 引言
由于海洋环境的复杂性,以声呐信号为基础的水下信号的自动化识别的分类是一种复杂的问题。人类专家进行的鉴别工作通常不是一种简单的任务而且有十分庞大的工作量。具有自适应和计算优势的神经网络的出现是十分适合有源声呐的分类。Gorman和Sejnowski[1]所作的开创性论文有可能是记载神经网络在该领域应用的首篇论文。他们用简单特性的频谱作为神经网络分类器的输入去从定位在海洋底部沙层上柱状形的岩石中区分出水雷。在这些开创性的论文后,人们已经对利用网络进行声呐目标的自动识别产生了浓厚的兴趣。多层感知器分类器[1]―[7]、径向基函数网络[3]、[8]、通用回归神经网络[9]和随机性神经网络[3]、有效的前馈性神经网络在文献科研中已经广泛的应用在识别声呐信号里。特征抽取是进行复杂信号例如视觉、语音鉴别或者在声呐反馈里目标探测中被提及的问题的分类的重要预处理步骤。这些问题的输入维数对于分类来说变成不利因素,如主元分析和神经鉴别分析。特征抽取技术把高因次信号降低为在特征空间里保存最有利用价值和相关联信息的低因次特征置位。在[10]、[11]中,一些特征提取技术应用在预先给予的声呐信号中。在这篇论文中,通用回归神经网络已经被应用于鉴别在海洋底部沙层上的一个水雷和柱状形岩石两个不同目标的反馈声呐。这里重点不仅是分类器本身而且在于应用主元分析的特征抽取技术的方法,可以改善分类器的性能。接受器工作特性分析是一种在声呐研究中测试诊断性能的既定的方法。
2. 关于Gorman和Sejnowski的数据
Gorman和Sejnowski[1]、[2],采用的最初声呐数据。这些数据组是从加里福尼亚大学机械研究数据库采集中心取得的。这些数据包含从两个来源:一个金属柱面和相似形的岩石中收集来的声呐反馈,两个目标放在同一个沙层平面上,以不同的视界角向它们发射声呐线性固频脉冲,从而产生变差的数据。在G&S的实验里,数据经过过滤和从中提取60个抽样(输入或者我们的维数)的频谱包络线。这些数据包含有111个从远离不同视界角和不同条件下跳动出来的声呐信号中获取的图案和97个在类似条件下的岩石中获取的图案。数据组包含有从90度幅宽的柱面和180度幅宽的岩石的不同视界角变体中获取的数据。在这些数据文件里共有208种抽样,这些被挑选出来的抽样增加了视界角的数目。
3. 通用回归神经网络在声呐目标分类中的应用
通用回归神经网络是基于概率密度函数估计的,有记忆基础的前馈型网络。通用回归神经网络上一种径向基函数网络,它经常应用在函数概算中,快速导流数次通用回归神经网络的特性能进行非线性函数建模,已经在给予足够数据的噪声环境中其出色完成任务的实验中得到证明。最初它在统计文学中得到发展,又以纳达亚―沃森积分方程的影响函数回归而闻名。在1990年D onald specht又重新发掘了它,通用回归神经网络拓扑结构包含四层:输入层、隐蔽层、总领层和输出层。通用回归神经网络的最大优点在于网络能被导流的速度,导流一种通用回归神经网络在一次完整的工作循环中可被完成。它不需要一种如在多层感知器那样的叠接导流程序,它近似一些在输入和输出向量之间的随机函数,可直接从导流数据中得出这函数的概率,而且它具有一致性,那就是,当导流设备的尺寸过大时伴随着对函数的微弱干扰,其估计错误率近似为零。像在标准回归方法中,通用回归神经网络应用在连续变量的估计中,它涉及到径向基函数网络,基于一种叫做拓扑结构回归的标准型统计方法。
通用回归神经网络体系结构如数字图1所示,有关通用回归神经网络体系结构和一些数学计算方面的详细信息在Specht的论文[3]中可得到验证。
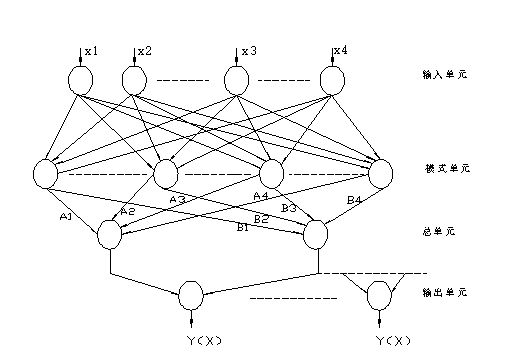
数字图.1. 通用回归神经网络体系结构
4.传统主元分析
主元分析是一种数据压缩和特征抽取的多变量统计分析方法,需要分类器在线操作中有直观实际应用。通过发送输出数据到m导向偶极子数量的简化上从而降低n维输入空间的维数,对于分类器设计来说其是一种有吸引力的方法,更便利于分类器的工作。主元分析在特征向量(从处理协变式的矩阵中计算)的基础中描绘原始数据空间,在对特征向量指示器处理过的能量进行相应的特征值计算中,考虑到最高特性值的m特征向量被数据传送所限制,一种有效的最少信息丢失的原始输入空间的维次简化方法被实现啦!有关主元分析详细计算可参阅[14]。
5.仿真结果
研究的目的是使通用回归神经网络从事于声呐反馈的鉴别,从而改善其分类性能和简化网络的复杂性。主元分析作为特征抽取方法被应用,通过MATLAB 6.0 和神经网络工具箱完成分类工作。数据组包含有208条反馈信息(其中111条柱形水雷反馈信号和97条岩石反馈信号),全部数据组等信号区分为随机训练组和测试组,(103种抽样为训练文件、105种抽样为测试文件)。此处作用的网络是一种全相连的前馈型包含60个输入波和1个输出波的神经网络。
研究的第一步,不含应用特征抽取方法的通用回归神经网络已经被应用在声呐数据中。扩展参数的抉择十分适合通用回归神经网络的特性,扩展数值选在0.06最佳,不含运用主元分析的通用回归神经网络分类器所实现的性能,如表一所示:
表一:不含运用主元分析的通用回归神经网络的正确分类百分率
等级 总数
“水雷”评估正确率% “岩石”评估正确率% 分类评估正确率%
训练100 训练100 训练100
测试92.06 测试90.48 测试91.42
第二步,主元分析已经应用在了有60维数输入空间的数据组中。当运用主元分析处理60维数输入空间简化为20维数的输入空间时,关于测试结果的最大准确度实现时,相同扩展数值通用回归神经网络分类器的分类性能如表二所示:
表二:含运用主元分析的通用回归神经网络分析正确分类百分率
等级 总数
“水雷”评估正确率% “岩石”评估正确率% 分类评估正确率%
训练100 训练100 训练100
测试93.65 测试92.85 测试93.33
表一与表二的结果相比显示,通用回归神经网络分类器的分类性能通过运用主元分析可得到改善,同时,主元分析提供用于在线通用回归神经网络分类器操作使计算的复杂性得到简化。
最后,接受器的工作特性以及被应用在通用回归神经网络分类器的测试结果中,接受器的工作特性分析在声呐探中的评估标准,表明探测的可能性交替使用与误差探测可能性的比值。对接受器的工作特性分析的诊断对测试差值来讲灵敏度和特征值是基本的表达式。计算如表三所示,表三中左边为分类结果,上部为有/无水雷状况。
表三: 诊断测试解析表
水雷扫描
岩石扫描
“水雷”分类器的结果
真实值
理想值
“岩石” 分类器的结果
错误偏差
真实偏差
真实值:59 理想值:3 错误偏差:4 真实偏差:39
灵敏度=
比功率=
6.结论
此文,通用回归神经网络已经应用于鉴别从两个来源:一个金属柱状物和相似形岩石收集来的水下目标。这里重点不仅是分类器本身而且是在于用主元分析改善分类器性能的特征抽取方法的处理。通过主元分析实现的简化计算复杂性的方法有助于小型神经分类器的设计开发。这种分类器设计有利于在线操作和在硬件方面可得到保证。当通用回归神经网络就分类成功率而论的运用特性相比以前的研究时,相比那些最大准确率可达90.4%[1]和接受器工作性能分析相似于1(灵敏度和比功率)所示的分类可靠性而言时其效果更好。
参考文献:
1. Gorman R.P.;Sejnowski T.J.,(1988). Learned classification of sonar targets using a massively parallel network. IEEE Transaction on Acoustics, Spech, and Signal Processing, Vol. 36, No.7,pp. 1135-1140.
2. Gorman R.P.;Sejnowski T.J.,(1988). Analysis of hidden units in a layered network trained to classify sonar targets. Neural Netwoeks, Vol 1,No1,pp.75-89.
3. Chen, C.H.(1992). Neural Netwoeks for active sonar classification. Pattern Recogceedings., Vol.II. Conference B :Pattern Recognition Methodology and Systems, Proceedings.,11th IAPR International Conferene on,pp. 438-440.
4. Diep, D.; johannet, A.; Bonnefoy, P.; Harroy, F.; Loiseau, P., Classification of sonar data for a mobile robot using nearal network .(1998) Intelligence and Systems, Proceedings., IEEE International Joint Symposia on, pp. 257-260.
5. Haley ,T.B.,(1990). Applying nearal network to automatic activ classification. Pattern Recognition, Proceedings ., 10th International Conferene on,Vol: 2, pp. 41-44
6. Shazeer, D.J.; Bello, M.G., Minehunting with multi-layer perceptrons. (1991) Neural Network for Ocean Engineering ,1991, IEE Conference on ,pp. 57-68.
7. YuWang Jing; EI-Hawaey, F.;A multilayered ANN architecture for underwater target tracking.(1994). Electrical and Computer Engineering , Conference Proceedings. 1994 Canadian Conference on, Vol .2pp. 785-788.
8. Yegnanaray,B.; Chouhan,H.M.; Chandra Sekhar, C., sonar target recoginting using radial basss functiong networks. (1992). Singapore ICCS\ISITA ’92. ‘Communications on the Move’, vol.1,pp.395-399.
9. Kapanoglu B., Yildmm T., Generalized Regression Neural Netwoeks Ror Underwater target Classification. Neu-Cee2004 2nd International Symposia on Electrical and Computer Engineering, Nicosia ,North Cyprus, pp:223-225.
10. Soares �CFilho, W.; Manoel de Seixas, J.;Perira Caloba, L.; Principal componefnt analysis for classifying passive sonar sigals.(2001). Circuits and Systems ,ISCAS 2001. The 2001 IEEE International Symposia on,Vol. 3, pp. 592-595.
11. Larkin ,M.J.; Optimal feature extraction techniques to improve Classification performance , with application to sonar signals .(1997) Neural Networks for Signal Processing VII .Proceedings of the 1997 IEEE Workshop ,pp. 64-71.
12. Woods, k.s.; bowyer,K.W., Generating ROC curves for artificial neural networks .(1994) Computre-Based Medical Systems, Proceedings 1994 IEEE Seventh Symposium on, pp. 201-206.
13. Specht D.F.,(1991) Ageneralized regression neuralnetwoeks . IEEE Transations on Neural Networks .Vol. 6, pp. 568-576.
14. Song W.; Shaowei X., ROBUST PCA Based on Neural Networks .(19970 Proceedings of the 36th Conferenc on Decision&Control San Diego , California USA ,pp.

