NURBS样条曲面建模方法
style="text-align: justify; text-indent: 2em; margin-top: 0px; margin-bottom: 0px; -ms-text-justify: inter-ideograph;">构强度退化系数和参数的变异性对结构的可靠度具有一定的影响,随机参数的变异系
数越大,结构的可靠度越小。
,
NURBS样条曲面建模方法
NURBS(非均匀有理B样条)是一种计算机处理几何信息的数据交换的工业标准,是一种强有力的几何设计工具[1]。NURBS在解析自由曲面时有直观的数学表达式,交互性强,采用NURBS方法建立的几何模型可以用于结构材料的仿真计算,特别是NURBS基函数具有协调性,可以作为有限元计算的基函数,实现等几何有限元计算。在等几何模型的构建和分析计算中,NURBS基函数、NUEBS曲线曲面建模及NURBS基函数求导过程如下:
(1) B样条基函数
令序列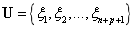 为一个单调不减序列,其中
为一个单调不减序列,其中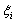 表示第i个节点,其中
表示第i个节点,其中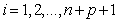 ,n为基函数的个数,p表示B样条基函数的阶数,则系列
,n为基函数的个数,p表示B样条基函数的阶数,则系列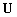 称为B
称为B 样条基函数的节点矢量。若节点矢量
样条基函数的节点矢量。若节点矢量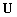 的头部与尾部元素各重复p+1次,则称该节点矢量为开节矢量,文中使用到的矢量就是开节矢量,开节矢量表示为:
的头部与尾部元素各重复p+1次,则称该节点矢量为开节矢量,文中使用到的矢量就是开节矢量,开节矢量表示为:
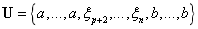
其中a和b均重复p+1次。
用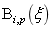 表示第i个p次B样条曲线基函数,给定了节点矢量之后,B样条基函数可以使用递推式给出。
表示第i个p次B样条曲线基函数,给定了节点矢量之后,B样条基函数可以使用递推式给出。
当p=0时:
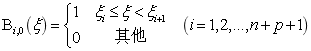
当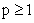 时:
时:
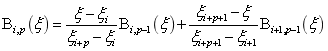
定义基函数个数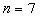 ,阶数
,阶数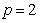 ,节点矢量
,节点矢量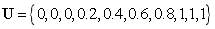 的B样条基函数,其函数图形如下:
的B样条基函数,其函数图形如下:
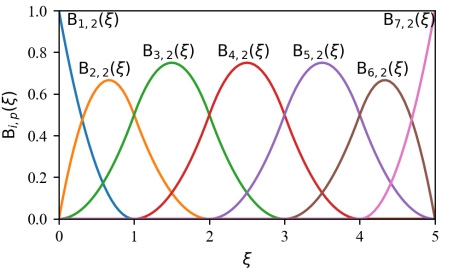
图1 非零二阶B样条基函数
由图1和B样条基函数的定义可以知道其具有如下性质:
Ⅰ、单元分解性,对任意的区间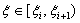 满足:
满足: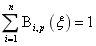 ;
;
Ⅱ、局部支撑性质,即仅在区间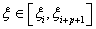 内不为0;
内不为0;
Ⅲ、基函数在端点处具有插值性,其他节点处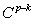 连续(节点重复度为
连续(节点重复度为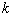 ,
,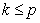 )。
)。
根据B样条基函数的递推式(1)和(2),可以计算基函数的导数。
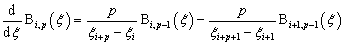
(2) NURBS曲线和曲面
利用B样条可以方便地对自由形状进行建模,但是不能精确表示一些简单的形状,如圆和椭球体,因此,在CAD建模中,使用的是B样条的泛化,即NURBS样条。NURBS样条是通过B样条的有理化形成的,具有B样条的特性和能精确表示简单形状的特性。NURBS曲线和曲面的创建方法如下:
(一)对于一条p次n个基函数的NURBS样条曲线,定义在节点矢量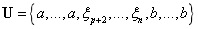 上的NURBS样条基函数用
上的NURBS样条基函数用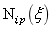 表示,其形式如下:
表示,其形式如下:
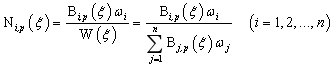
其中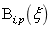 为第
为第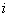 个
个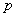 次有理B样条基函数;
次有理B样条基函数;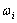 为NUEBS权重。
为NUEBS权重。
给定n个控制点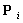 (
(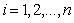 ),可以得到样条曲线
),可以得到样条曲线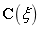 的表达式为:
的表达式为:
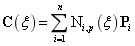
式中: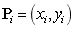 表示二维空间中的第i个控制点。
表示二维空间中的第i个控制点。
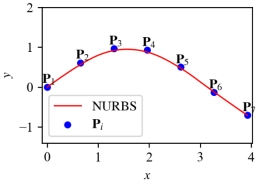
取p=2,n=7,给定控制点序列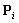 (
(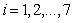 ),可得到NURBS样条曲线如图2(a) 所示,将其中的一个控制点
),可得到NURBS样条曲线如图2(a) 所示,将其中的一个控制点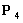 移动一个位置,NURBS样条曲线的形状也随之改变,如图2(b)所示。
移动一个位置,NURBS样条曲线的形状也随之改变,如图2(b)所示。
(a) 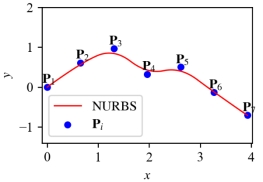
(b)
图2 NURBS样条曲线
(二)对于一张定义在u方向的p次,v方向q次的NURBS曲面,其基函数的个数为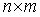 个,给定节点矢量
个,给定节点矢量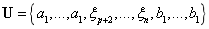 和
和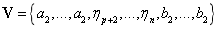 ,该NURBS曲面的基函数为:
,该NURBS曲面的基函数为:
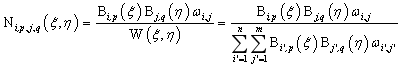
其中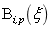 为第
为第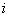 个
个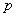 次有理B样条基函数;
次有理B样条基函数;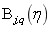 为第
为第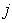 个
个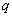 次有理B样条基函数;
次有理B样条基函数;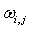 为NURBS权重。
为NURBS权重。
给定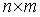 个控制点
个控制点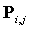 (
(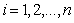 ,
,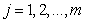 ),可以得一个NURBS曲面
),可以得一个NURBS曲面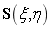 的表达式为:
的表达式为:
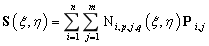
式中: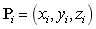 表示三维空间中的第i个控制点。
表示三维空间中的第i个控制点。
NURBS样条基函数也具有规范性,满足: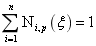 或
或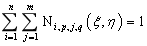
由于NURBS样条基函数满足任意曲线和曲面的建模,并且满足有限元形函数的协调性要求,可以在有限元分析中作为形函数进行等几何分析。
(3) NURBS实体
与NURBS曲线和曲面类似,定义一个在u方向p次,v方向为q次,w方向为r次的次的NURBS实体,其基函数的个数为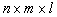 个,给定B样条基函数的节点矢量
个,给定B样条基函数的节点矢量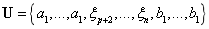 和
和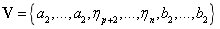 ,
,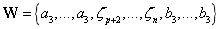 ,组合得到NURBS实体的基函数为:
,组合得到NURBS实体的基函数为:
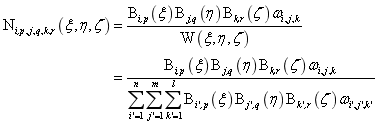
其中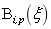 为第
为第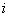 个
个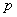 次有理B样条基函数;
次有理B样条基函数;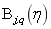 为第
为第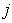 个
个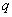 次有理B样条基函数;
次有理B样条基函数;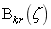 为第
为第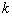 个
个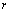 次有理B样条基函数;
次有理B样条基函数;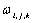 表示NURBSqu权重。
表示NURBSqu权重。
同理,给定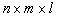 个控制点
个控制点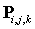 (
(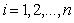 ,
,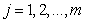 ,
,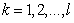 ),可以得一个NURBS实体
),可以得一个NURBS实体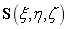 的表达式为:
的表达式为:
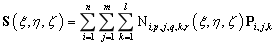
(4) NURBS曲面外形调整方法
NURBS曲面具有很好的局部修改性,为建模和计算提供了良好的特性。对NURBS曲面外形的修改就是移动其控制点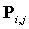 ,或者修改其权重
,或者修改其权重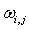 ,修改后仅影响
,修改后仅影响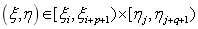 内部那部分曲面的形状
内部那部分曲面的形状
取p=2,q=2,n=5,m=5,并且给定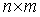 个控制点
个控制点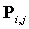 如图3(a)所示,可以得到一个NURBS曲面如图3(b),可以通过改变其中控制点的位置改变曲面的形状,如图3(c)所示移动其中的一个控制点
如图3(a)所示,可以得到一个NURBS曲面如图3(b),可以通过改变其中控制点的位置改变曲面的形状,如图3(c)所示移动其中的一个控制点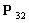 ,NURBS曲面将发生变化,如图3(d)所示。
,NURBS曲面将发生变化,如图3(d)所示。
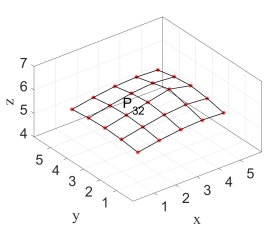
(a) 初始控制点系列
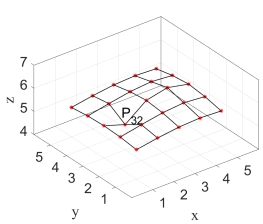
(b) 移动其中一个点后控制点系列
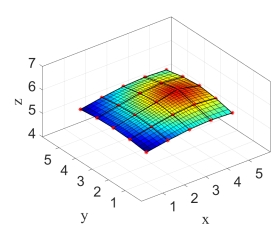
(c) 初始NURBS曲面
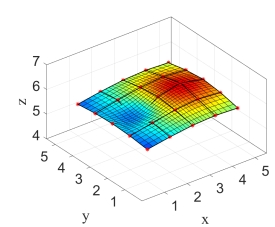
(d) 调整后的NUEBS曲面
图3 移动控制点调整NURBS曲面
(5) NURBS基函数导数
NURBS曲面是光滑可导的,其曲面方程具有良好的可微性,构成NURBS曲面方程的B样条基函数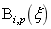 在节点处
在节点处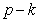 次连续可微,
次连续可微,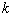 为该节点的重复度,在节点期间内部
为该节点的重复度,在节点期间内部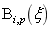 无限次可微。
无限次可微。
根据B样条基函数的求导公式,一维NURBS求导公式为:
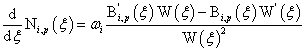
其中:
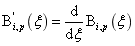
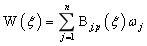
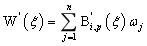
在等几何分析中,雅可比矩阵的求解需要用到NURBS基函数的导数。
二维NURBS求导公式为:
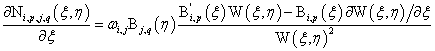
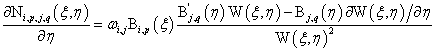
其中:
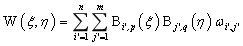
三维NURBS求导公式为:
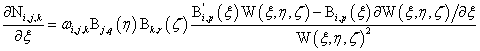
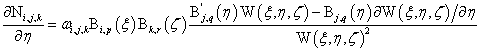
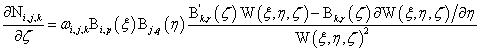
其中:
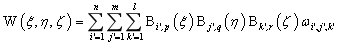
(6) 计算域的细化
等几何有限元方法是一种数值计算的方法,获得的计算结果为问题的近似解,为了提高计算的精度,需要对模型进行细化。对于NURBS样条曲线或曲面,需要在不改变原几何模型的基础上进行细化网格。常用的细化方法有三种,分别是h细化(插入节点的方法)、p细化(提升NURBS基函数阶数的方法)和k细化(节点插入和升阶)。
① h细化:
插入节点的方法是在不改变模型的几何形状的基础上通过插入节点来增加节点矢量的长度。假设有节点矢量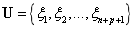 ,在期间
,在期间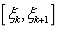 中插入一个新的节点
中插入一个新的节点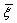 ,获得新的节点矢量
,获得新的节点矢量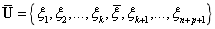 ,可知
,可知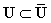 ,新的基函数由式(1)和式(2)迭代计算,通过原控制点
,新的基函数由式(1)和式(2)迭代计算,通过原控制点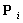 (
(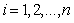 )计算新的控制点
)计算新的控制点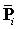 (
(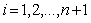 ),计算公式如下:
),计算公式如下:
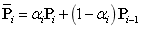
其中
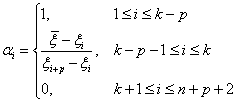
根据NURBS基函数的求导公式,节点矢量中存在的节点可以重复,但是节点重复时基函数的连续性会被削弱、NURBS曲线或曲面的光滑程度也会被削弱。通过上式来添加控制点数量,每个控制点出现的次数不能超过p次,否则曲面或者曲面将会变得不连续。
② p细化
p细化是在不改变NURBS基函数个数和几何参数的前提下提高基函数的阶数,在p细化过程中,节点矢量中的唯一节值必须重复,从而确保曲线或曲面的p阶导数不连续。新的控制点数量取决于现有的节点的多重性。
与h细化的情况一样,提升基函数的阶数构成的解空间包含原解空间。在不改变样条曲线或曲面几何形状的前提下提高基函数的多项式阶数可以使曲线的参数化保持不变。
p细化包含以下三个步骤:Ⅰ、插入节点,使节点的重复度变为p,这样可以高效地将原曲线或曲面划分为多段Bezier曲线;Ⅱ、提高Bezier曲线的阶数;Ⅲ、消除多余的节点并将多段曲线或曲面组合成一部分。
③ k细化
k细化是等几何分析中最常用的细化方法,并且是等几何有限元分析独有的细化方法,充分利用了p细化和h细化互不干涉的性质。因此k细化有两种不同的细化流程:第一种是先进行节点插入再提升阶数;第二种是先进行阶数提升再进行节点插入。两种方法中,先提升阶数再插入节点的细化方法得到的曲线或者曲面在相同参数点的连续性更高。
T样条曲面建模方法
NURBS样条曲面市工业几何形状表达的唯一标准,但是存在一定的缺陷,主要表现为如下两个方面的问题:①控制网格的每一行或每一列的控制点数量必须相同,导致产生大量的冗余点;②单张NURBS曲面无法表达复杂曲面,在裁剪拼接过程中会产生裂缝和褶皱等现象。T样条曲面为了解决上面出现的两个问题,T样条曲面的控制点不需要满足每一行或每一列控制点数量必须相同,在节点处存在中断现象,类似于英文大写字母“T”,所以被命名为T样条曲面(参考文献《基于NURBS的符合材料构建多尺度建模技术研究》中的参考文献:[41,42,43,44]。
等几何有限元
等几何有限元分析的步骤:
(1)总体结构的离散化:构建并输入结构的CAD模型,使用NURBS曲线或曲面将整体结构离散成有限个单元,即生成NURBS网格,并对其进行细化。结构离散化需要的信息包括:曲面阶数、节点矢量和控制点等。
(2)单元力学分析:设定材料的物理性质,在每一个NURBS单元上施加力学的控制方程。在单元内部使用Gauss-Legendre数值积分求解任意点的数值。遍历所有高斯点后获得单元刚度矩阵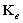 。
。
(3)组装总体刚度矩阵:遍历所有NURBS单元之后,组装单元刚度矩阵获得模型结构的总体刚度矩阵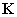 。
。
(4)施加边界条件并求解:在得到总体刚度矩阵后,施加约束、力或位移的边界条件,求解方程:
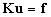
(5)后处理:计算获得总体结构每个节点的位移向量。
(一)积分计算:
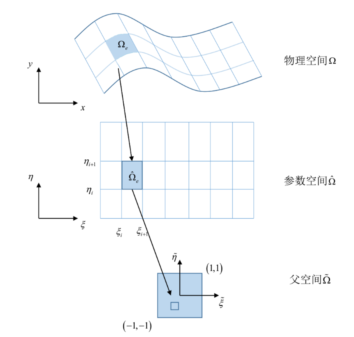
与有限元形函数一样,等几何有限元分析使用等参单元的方法进行,给定局部坐标系的规则单元,通过映射的关系,获得物理坐标系的复杂单元,其中涉及到了多个空间的联系,包括物理空间、参数空间和父空间。其中物理空间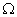 是真实几何模型空间,采用坐标
是真实几何模型空间,采用坐标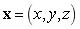 表示;参数空间
表示;参数空间 由节点向量中的非零区间组成,也可以称为NURBS原象空间。采用坐标
由节点向量中的非零区间组成,也可以称为NURBS原象空间。采用坐标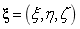 表示,并且由于参数空间是由节点向量中不相等的节点组成,可以将其简化为单位空间;父空间
表示,并且由于参数空间是由节点向量中不相等的节点组成,可以将其简化为单位空间;父空间 是数值积分计算时定义的空间,即:
是数值积分计算时定义的空间,即: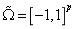 ,其中
,其中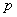 为空间维度。
为空间维度。
空间的映射关系:
对于曲线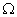 ,使用单变量的NURBS基函数作为形函数,即
,使用单变量的NURBS基函数作为形函数,即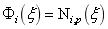 ,对于曲面
,对于曲面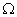 ,使用双变量的NURBS基函数作为形函数,即
,使用双变量的NURBS基函数作为形函数,即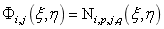 。
。
以NURBS二维曲面为例,其物理空间与参数空间的映射关系为:
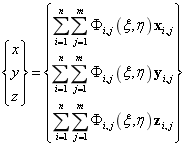
物理空间和参数空间映射的雅可比行列式:
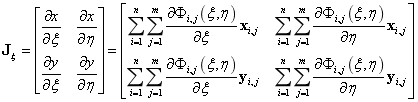
物理空间形函数导数的表达式为:
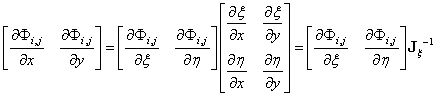
其中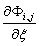 和
和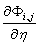 都是采用NURBS基函数求导计算公式计算的。
都是采用NURBS基函数求导计算公式计算的。
对于NURBS参数空间的基本单元: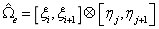 ,与父域
,与父域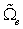 的映射关系为:
的映射关系为:
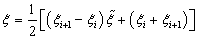
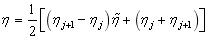
其中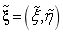 表示父空间的坐标。
表示父空间的坐标。
参数空间和父空间的映射的雅可比行列式为:
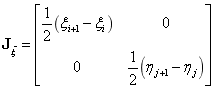
要在整个物理空间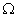 中对方程
中对方程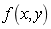 进行积分,可以将计算离散到基本的几何单元
进行积分,可以将计算离散到基本的几何单元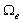 中进行计算,进而通过映射到参数空间
中进行计算,进而通过映射到参数空间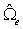 与父空间
与父空间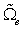 中,使用Gauss-Legendre积分进行计算。
中,使用Gauss-Legendre积分进行计算。
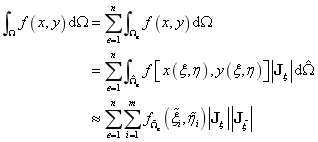
式中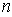 表示积分单元的个数,
表示积分单元的个数,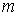 表示积分单元内高斯点的个数,
表示积分单元内高斯点的个数,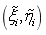 表示高斯积分点坐标。
表示高斯积分点坐标。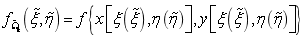 表示使用父单元坐标
表示使用父单元坐标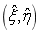 为参数的方程,其转换关系如式和式所示。
为参数的方程,其转换关系如式和式所示。
(二)计算刚度矩阵
对结构的位移同样使用NURBS作为插值形函数表示,如下所示:
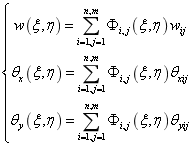
式中,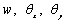 分别表示板壳结构厚度方向的位移和x及y方向的旋转位移;n和m分别表示板壳x和y方向的NURBS基函数的个数;
分别表示板壳结构厚度方向的位移和x及y方向的旋转位移;n和m分别表示板壳x和y方向的NURBS基函数的个数;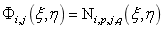 表示二维NURBS基函数;
表示二维NURBS基函数;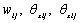 分别表示控制点处板壳结构厚度方向的位移和x及y方向的旋转位移。
分别表示控制点处板壳结构厚度方向的位移和x及y方向的旋转位移。
使用矩阵形式表示为:
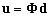
其中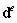 为控制点的位移向量,
为控制点的位移向量,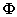 为NURBS 基函数矩阵,其形式如下所示:
为NURBS 基函数矩阵,其形式如下所示:


由于Mindlin板考虑了横向剪切变形,其应变如下所示:
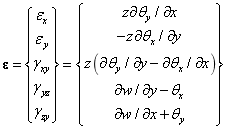
将位移使用控制点的插值表示:
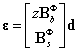
上式中,z表示物理坐标系下板壳z轴方向的坐标,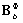 和
和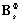 分别表示弯曲应变矩阵和剪切应变矩阵,跟有限元方法中的应变矩阵类似,其表达式如下所示:
分别表示弯曲应变矩阵和剪切应变矩阵,跟有限元方法中的应变矩阵类似,其表达式如下所示:
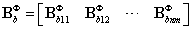
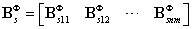
其中:
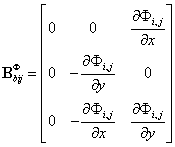
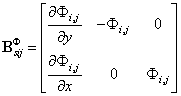
应力的表达式为:
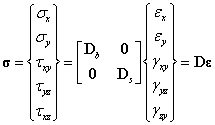
其中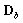 和
和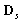 分别表示弯曲弹性矩阵和剪切弹性矩阵,表达式如下所示:
分别表示弯曲弹性矩阵和剪切弹性矩阵,表达式如下所示:
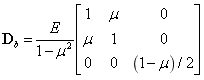
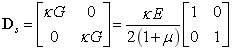
上式中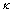 为剪切修正因子,对各向同性材料,取
为剪切修正因子,对各向同性材料,取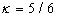
由此可得刚度矩阵为:
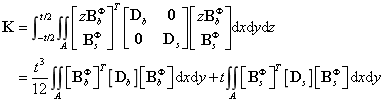
式中,t表示板壳的厚度。
利用式的积分方法对式进行积分,获得结构等几何刚度矩阵。
(三)计算质量矩阵及阻尼矩阵
质量矩阵是对连续分布的质量的离散化表达,常用的质量矩阵有一致质量矩阵和集中质量矩阵两种。其中一致质量矩阵式正定的非对角矩阵,需要通过插值形函数积分获得;集中质量矩阵为对角矩阵,优点是计算简单计算量小。对于梁和板壳结构,一致质量矩阵计算得到的结果较为准确,本文中使用一致质量矩阵计算板壳等几何方程中的质量矩阵,其计算公式如下所示:
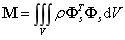
上式中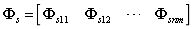 ,其中:
,其中:
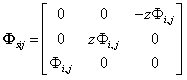

利用式的积分方法对式进行积分,获得结构等几何质量矩阵。
等几何有限元热结构计算
平板结构的热平衡方程
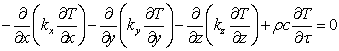
边界条件(z方向的热流变化等于太阳光的照射产生的热流输入和辐射散热之差):
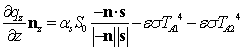
由于考虑热流在板壳结构中是三维传导的,因此需要将表示板壳结构的NURBS曲面基函数扩展到能够表示厚度的三维基函数,使用表示参考面的二维NURBS基函数和厚度方向的一维NURBS基函数组合表示温度场的插值基函数,其表达式如下所示:
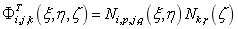
利用式将温度场表示为:
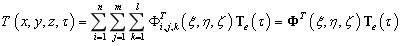
使用Garlerkin法在单元内对热平衡方程进行积分得:
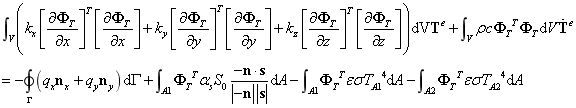
可将上式简化为
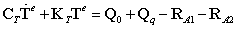
其中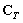 为热容矩阵;
为热容矩阵;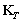 为热刚度矩阵;其表达式如下所示
为热刚度矩阵;其表达式如下所示
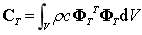
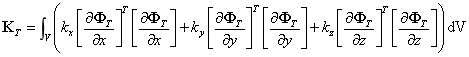
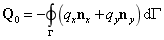
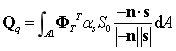
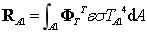
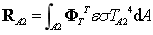
热载荷计算
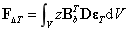
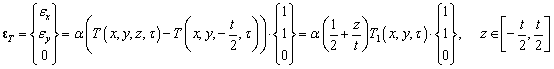
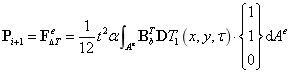
添加随机场
随机等几何分析:
随机刚度矩阵如下所示:
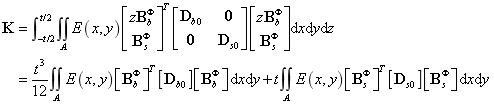
上式中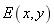 表示弹性模量的随机场,
表示弹性模量的随机场,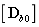 和
和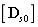 表示单位弹性矩阵,即将常规弹性矩阵的弹性模量用1表示。
表示单位弹性矩阵,即将常规弹性矩阵的弹性模量用1表示。
由于需要在参数空间中进行积分计算,需要计算参数空间中的弹性模量随机场: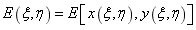 ,式可变为:
,式可变为:
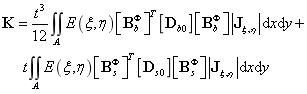
上式中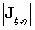 表示物理坐标与参数坐标变换的雅可比行列式。
表示物理坐标与参数坐标变换的雅可比行列式。
添加的随机场有:弹性模量E,质量密度 与热膨胀系数
与热膨胀系数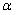
等几何有限元与普通的有限元方法的区别:与用插值函数作为有限元形函数的方法相比,使用NURBS基函数作为形函数导致控制节点通常不在实体上,对于板壳单元,控制节点通常不在其参考平面上,给节点处的坐标系建立以及后续对位移场的插补带来困难。
参考文献
[1] Piegl,L. Tiller,W. The NURBS Book[M] Springer-Verlag. 1997.
航空航天器在运行过程中处于复杂的空间环境,恶劣工况导致结构发生振动从而影响航天器的正常工作。特别地,结构参数如弹性模量会随着环境温度的变化而改变,从而进一步引起结构振动特性及其响应的变化。故分析结构在多场环境下的动力响应及其可靠性问题具有现实的工程背景和重要的理论意义。本文以航天器中的常用结构
单元-薄壁圆管为研究对象,考虑其在太阳照射的持续热流作用下,由于温度变化引
起的热-结构耦合振动进而带动结构内部的空气一起振动,使流体与结构之间发生相
互相用,最终形成热-结构-噪声三场耦合的现象。并在考虑结构参数的随机性时,对
结构的随机动力响应及其动态可靠性进行了研究。本文的主要工作如下:
(1)基于查阅的国内外相关文献,总结了结构在热-结构耦合,结构-流体耦合等
情况下的动力响应研究理论、研究方法等现状以及目前仍存在的问题;进一步回顾了
热力学、流体力学、结构动力学以及有限元等基础理论知识,为后续的研究内容奠定
理论基础。
(2)本文在第三章中首先构建了确定性结构在热-结构-声三场耦合下的动力学
模型,具体过程为:首先将温度场用平均温度场和扰动温度场来表示并构建对应的热
传导有限元方程,其次将热振动引发的声场进行离散化构建出声场有限元方程,进而
得到结构在热-结构-声耦合下的动力学方程;之后对三场耦合动力学方程进行求解,
具体方法为:对时间域内的温度场、结构动力响应和声场进行交替迭代计算,其中温
度场采用牛顿迭代法和时间差分法来求解,采用Newmark积分法获得结构的动力响
应,基于龙格-库塔法求解声场的响应。
进而,考虑温度场和结构参数的随机性时,基于三场耦合下确定性结构的动力响
应分析过程,求出了各动力响应的数字特征值。具体为:将结构的物理参数,几何参
数以及初始热流等视为正态分布的随机变量,基于灵敏度的矩法首先构建出结构温度
场的随机模型,并进一步通过随机因子法和代数综合法构建了结构动力学随机模型,
推导出结构位移和应力响应的均值和均方差。最后,采用数值算例对所提方法的可行
性和有效性进行了验证;其中考察了不同参数的随机性对结构响应随机性的影响,并
通过蒙特卡洛法进行结果对比,并对确定性结构以及随机结构的动力响应随时间变化
的曲线图进行了分析。结果表明:结构在热-结构-声耦合下会发生颤振,且随着时间
的推移,结构的动力响应幅值会随之增大;弹性模量,质量密度对结构响应的分散性
的影响较为明显,且随机参数的变异系数与结构响应的分散性成正比。
(3)在第三章研究结果的基础上,在这一部分,对三场耦合下薄壁圆管结构在
交变平均温度场和交变扰动温度场下的疲劳失效问题进行了研究。首先将交变平均温度以及声压产生的疲劳应力转化成等幅随机荷载,将交变扰动温度场以及声压产生的
疲劳应力等效为变幅随机荷载。综合应用疲劳累积损伤理论和剩余强度模型,将两种
随机载荷统一,并采用应力-强度干涉理论推导出结构的极限状态方程,进而推导出
结构的动态可靠度指标,并通过算例分析了结构在不同循环次数下的动力可靠度。研
究结果表明:结构在热-结构-声耦合下的疲劳可靠性具有“突然死亡”的特点,且结
全套毕业设计论文现成成品资料请咨询微信号:biyezuopinvvp QQ:1015083682
返回首页
如转载请注明来源于www.biyezuopin.vip

