逻辑斯蒂回归实验

逻辑斯蒂回归
问题背景：
贝叶斯决策理论以及朴素贝叶斯都可以对样本进行分类，通过贝叶斯公式求出以该样本作为条件求出每个类的后验概率，找到最大化后验概率的类。这种方法思路清晰，但是步骤有些冗余，在类先验和类条件分布满足特定的条件时，可以推导出一个判别式模型，直接决定样本的分类。
Logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释。所以实际中最常用的就是二分类的Logistic回归。
实验原理：
逻辑斯蒂回归的分类器的判别式模型(二分类)：
P（Y=1|X=<X1,X2,….Xn>）=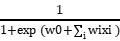
P（Y=0|X=<X1,X2,….Xn>）=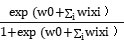
逻辑斯蒂回归的分类器的产生式模型：
在P(Y)（类先验）满足二项分布，P(Xi|Y=K)（类条件分布）满足高斯分布N（uik,σi）。
即X的每一维都独立于其它维，并且类类之间的相同维度的方差相同。（两个类共享同一个对角协方差矩阵）
P（Y=1）=π
P(Y=2)=1-π
P(Xi|Y=K)~N(uik,σi)
P(Y=1|X)=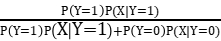
P(Y=1|X)=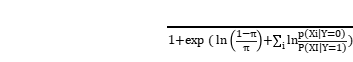
P（Y=1|X=<X1,X2,….Xn>）=   *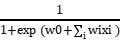
得到逻辑判别式模型*，利用该判别式模型我们可以很简便地对样本进行分类，而不必去计算每个类的后验概率并比较。
实验过程：
生成样本：由逻辑回归判别式的推导可知类条件分布为两个共享一个对象协方差矩阵的高斯分布。
为了验证模型的正确性，用两个高斯分布生成带类别标签的训练集和测试集，训练集训练好参数后，用训练后的模型对测试集进行分类，并与测试集数据的真实类别比较，计算模型分类的正确率
MLE
计算条件似然函数
L=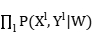
优化目标：
Wmcle=arg max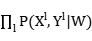
取对数：
l(W)=ln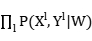
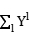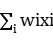l(W)=(w0+)-ln(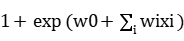
用梯度方法求解
wiwi+step*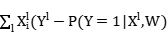
设置参数初始值

设置步长，迭代终止条件（计算优化目标的变化是否小于特定值）

迭代计算更新参数，若满足迭代终止条件则训练结束。

用训练完成模型给验证集分类，计算分类的正确率。

MAP
大部分步骤与MLE类似，因为假设W有一个先验W~N(0,σI)
优化目标改为：
W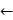arg max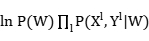
迭代式：
wi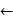wi+step*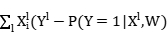-step*λwi
λ为一个和σ相关的数，对应着参数先验分布的具体情况，可根据自己对先验的预期来设置这个λ。


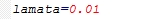
如果给MCLE的目标函数（最大化，若要得到最小化的优化目标损失函数，取负即可）对应的损失函数加上一个所有参数平方和形式惩罚，则也可以得到以上迭代式，说明先验对应着惩罚。
实验结果分析
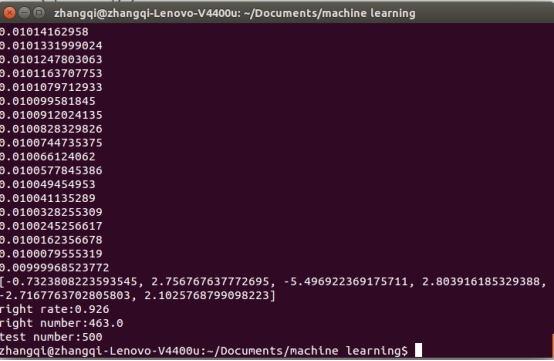
利用训练集得到的逻辑回归分类器在验证集上（500个）进行分类检测，测试分类正确的样本点数以及正确率。
调整实验参数，易发现，收敛的阈值设置的越小，则正确率越高，但是训练的时间越长。此外正确率还取决于生成样本那两个高斯函数均值的距离，以及方差的大小。
方差越大，模型分类的正确率就越低。

附录：实验完整代码
Lrmle
#coding:utf-8
import math
import copy
import numpy as np
import matplotlib.pyplot as plt
import random
dim=5
num=1000
testnum=500
sigma=[]
u1=[]
u0=[]
X=[]
W=[]
Xtest=[]
step=0.0001
Epsilon=0.01
def ini(sigma,u1,u0,X,Xtest,W):
for i in range(dim):
sigma.append(0.5)
u1.append(random.random())
u0.append(random.random())
for datanum in range(num):
a=[]
b=random.random()
if b>0.5:
for i in range(dim):
a.append(np.random.normal()*sigma[i] + u1[i])
a.append(1)
else:
for i in range(dim):
a.append(np.random.normal()*sigma[i] + u0[i])
a.append(0)
X.append(a)
for datanum in range(testnum):
a=[]
b=random.random()
if b>0.5:
for i in range(dim):
a.append(np.random.normal()*sigma[i] + u1[i])
a.append(1)
else:
for i in range(dim):
a.append(np.random.normal()*sigma[i] + u0[i])
a.append(0)
Xtest.append(a)
for i in range(dim+1):
W.append(1.0)
def Probr(X,W):
temp=0
for i in range(dim):
temp=temp+X[i]*W[i]
son=math.exp(W[dim]+temp)
return son/(son+1)
def l(W,X):
su=0
for datanum in range(num):
temp=0
for i in range(dim):
temp=temp+W[i]*X[datanum][i]
su=su+X[datanum][5]*(W[dim]+temp)-math.log(1+math.exp(W[dim]+temp))
return su
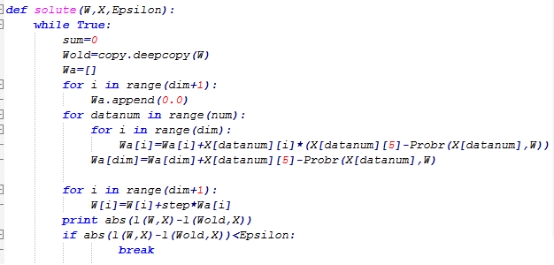
def solute(W,X,Epsilon):
while True:
sum=0
Wold=copy.deepcopy(W)
Wa=[]
for i in range(dim+1):
Wa.append(0.0)
for datanum in range(num):
for i in range(dim):
Wa[i]=Wa[i]+X[datanum][i]*(X[datanum][5]-Probr(X[datanum],W))
Wa[dim]=Wa[dim]+X[datanum][5]-Probr(X[datanum],W)
for i in range(dim+1):
W[i]=W[i]+step*Wa[i]
print abs(l(W,X)-l(Wold,X))
if abs(l(W,X)-l(Wold,X))<Epsilon:
break
if __name__ == '__main__':
ini(sigma,u1,u0,X,Xtest,W)
solute(W,X,Epsilon)
numright=0.0
for i in range(testnum):
Y1=0
tmp=Probr(X[i],W)
if tmp>0.5:
Y1=1
else:
Y1=0
if X[i][5]==Y1:
numright=numright+1.0
print W
print "right rate"+str(numright/testnum)
print "right number" +str(numright)
print "test number" +str(testnum)
lrmap
#coding:utf-8
import math
import copy
import numpy as np
import matplotlib.pyplot as plt
import random
dim=5
num=1000
testnum=500
sigma=[]
u1=[]
u0=[]
X=[]
W=[]
Xtest=[]
step=0.0001
Epsilon=0.01
lamata=0.01
def ini(sigma,u1,u0,X,Xtest,W):
for i in range(dim):
sigma.append(0.3)
u1.append(random.random())
u0.append(random.random())
for datanum in range(num):
a=[]
b=random.random()
if b>0.5:
for i in range(dim):
a.append(np.random.normal()*sigma[i] + u1[i])
a.append(1)
else:
for i in range(dim):
a.append(np.random.normal()*sigma[i] + u0[i])
a.append(0)
X.append(a)
for datanum in range(testnum):
a=[]
b=random.random()
if b>0.5:
for i in range(dim):
a.append(np.random.normal()*sigma[i] + u1[i])
a.append(1)
else:
for i in range(dim):
a.append(np.random.normal()*sigma[i] + u0[i])
a.append(0)
Xtest.append(a)
for i in range(dim+1):
W.append(1.0)
def Probr(X,W):
temp=0
for i in range(dim):
temp=temp+X[i]*W[i]
son=math.exp(W[dim]+temp)
return son/(son+1)
def l(W,X):
su=0
for datanum in range(num):
temp=0
for i in range(dim):
temp=temp+W[i]*X[datanum][i]
su=su+X[datanum][5]*(W[dim]+temp)-math.log(1+math.exp(W[dim]+temp))
return su
def solute(W,X,Epsilon):
while True:
sum=0
Wold=copy.deepcopy(W)
Wa=[]
for i in range(dim+1):
Wa.append(0.0)
for datanum in range(num):
for i in range(dim):
Wa[i]=Wa[i]+X[datanum][i]*(X[datanum][5]-Probr(X[datanum],W))
Wa[dim]=Wa[dim]+X[datanum][5]-Probr(X[datanum],W)
for i in range(dim+1):
W[i]=W[i]+step*Wa[i]-step*lamata*Wa[i]
print abs(l(W,X)-l(Wold,X))
if abs(l(W,X)-l(Wold,X))<Epsilon:
break
if __name__ == '__main__':
ini(sigma,u1,u0,X,Xtest,W)
solute(W,X,Epsilon)
numright=0.0
for i in range(testnum):
Y1=0
tmp=Probr(X[i],W)
if tmp>0.5:
Y1=1
else:
Y1=0
if X[i][5]==Y1:
numright=numright+1.0
print W
print "right rate"+str(numright/testnum)
print "right number" +str(numright)
print "test number" +str(testnum)