EM算法求解高斯混合模型

EM算法求解高斯混合模型
问题背景：
实际生活中的样本很多是无标签的我这些样本含有隐变量或者潜在变量。如果概率模型的变量都可以被观测到，那么可以直接使用极大似然法估计模型参数。但是当模型中含有隐变量的时候。就不能简单的使用这些估计方法。EM算法就是含有隐变量的概率模型参数估计的极大似然法。
实验原理：
GMM高斯混合模型。
模型假设：
假设X是由个高斯分布均匀混合而成的，这K个高斯分布有自己的均值，协方差矩阵。
每一个高斯混合模型中的样本点都是通过下面的策略生成的：
1. 在K个高斯混合模型中按照概率P（Y=i）选择一个高斯分布。
2. 这个点在属于第i个高斯分布的条件下概率分布为X ~ N(μi,σi).
即：
P(X|Y=i)~ N(μi,σi).
P（X）=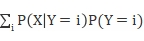
要优化的目标：关于X的边缘概率密度的似然函数。
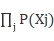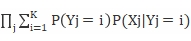=      （1）
要优化这个目标函数，有一系列的数值计算方法。例如对每个参数求偏导数，或者利用梯度下降，牛顿法等迭代办法。
事实上这些办法都是不可行的，梯度下降法选择步长很难办，不小心就不收敛了，要不然就太慢。求偏导数也不一定有解析解。
所以EM算法就出现了，它是一种处理含有隐变量数据的通用方法。
在选择参数的初始值之后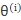开始进行迭代：
分为E步（Expectation）：
计算P（Y|X,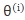）(在给定观测数据X和当前参数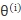的条件下隐变量Y的条件概率分布。
M步（Maximize）：
求使优化目标函数最大的新一轮的迭代的参数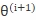
重复执行E步 ，M步，直到迭代收敛。
实验过程：
数据的生成：
实际运用中需要进行聚类的点是无标签的大量的数据。在本实验中，为了验证实现EM算法的正确性，生成数据的来源为K=2个高斯分布（Mu[1],Sigma[1]）,(Mu[2],Sigma[2])，这两个高斯分布有自己的参数，并以一定的概率选择由哪一个高斯分布生成样本(pi[1],pi[2])。

初始参数的选择：任意即可（Mu1,Mu2,Sigma1,Sigma2,pi1,pi2）.这些参数需要设置成全局的（global），以便在迭代步骤中随时改变。

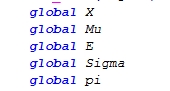
在EM算法求得结果以后和生成这些样本点的真实的参数做比较，从而验证算法以及程序的正确性。
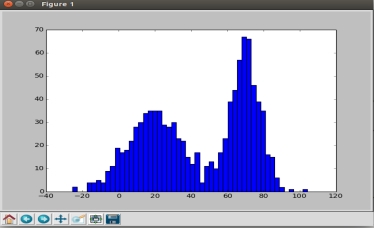
为了更明确的看出生成样本的分布，更方便的生成样本，该实验所有的样本均为1维，这样可以用绘制的直方图来清晰地看出样本分布。
E步：
计算在当前观测的数据X，参数（Mu1,Mu2,Sigma1,Sigma2,pi1,pi2）下隐藏变量Y的条件分布
E[i,j]表示第i个样本的隐藏变量Y=j,(j=1,2)在当前参数下的条件概率
E[i,j]=pij*P(Xi|Muj,Sigmaj),(j=1,2)
其中P(Xi|Muj,Sigmaj)可直接利用高斯分布的概率密度函数可计算。

M步：
求使目标函数（即（1）式，完全数据的似然函数关于在给定观测数据X和当前参数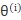下对隐变量Y的条件概率分布的期望）最大的参数。
我这里采用MLE

正如刘老师的ppt中所说（calls inference and fully observed learning as subroutines）.
Muj=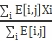
Sigmaj=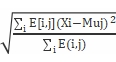
Pij=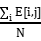
在迭代前后用新旧参数，观测样本计算，目标函数（1），如果前后增加的数量小于2.4e-100,退出迭代。
如果迭代超过一定次数，退出迭代。

实验结果分析
输出当前的参数，并与真实的参数，样本实际的分布进行比较。
一开始把收敛的阈值设置的较大（优化目标一次EM优化后的差值）（e-10左右），导致方差不能很好的预测，和真实的值差别较大。（没有完全收敛）
打印出每一步迭代对参数的更新结果后发现每一次迭代对参数更新的程度很大，但是对优化目标函数的影响却较小。说明EM方法对参数优化的速度非常快，与前实验多项式拟合中普通的梯度方法的速度形成鲜明对比。前实验中收敛阈值设置到e-10左右时，已经需要消耗近10个小时，而EM算法不到十次迭代便可达到e-300数量级。
由此可见EM算法在求解此类问题时的巨大优势。

附录实现的完整代码
#coding:utf-8
import math
import copy
import numpy as np
import matplotlib.pyplot as plt
isdebug = True
def ini_data(Sigma1,Sigma2,Mu1,Mu2,k,N):
global X
global Mu
global E
global Sigma
global pi
pi=[]
pi.append(0.5)
pi.append(0.5)
X = np.zeros((1,N))
Mu = []
Sigma=[]
Sigma.append(10)
Sigma.append(10)
Mu.append(1)
Mu.append(100)
E = np.random.random((N,k))
for i in xrange(0,N):
if np.random.random(1) > 0.5:
X[0,i] = np.random.normal()*Sigma1 + Mu1
else:
X[0,i] = np.random.normal()*Sigma2 + Mu2
if isdebug:
print X
def e_step(k,N):
global E
global Mu
global X
global Sigma
global pi
for i in xrange(0,N):
Denom = 0
for j in xrange(0,k):
Denom += pi[j]*math.exp((-1/(2*(float(Sigma[j]**2))))*(float(X[0,i]-Mu[j]))**2)
for j in xrange(0,k):
Numer = pi[j]*math.exp((-1/(2*(float(Sigma[j]**2))))*(float(X[0,i]-Mu[j]))**2)
E[i,j] = Numer / Denom
if isdebug:
print E
def m_step(k,N):
global E
global X
for j in xrange(0,k):
Numer = 0
mosig=0
Denom = 0
for i in xrange(0,N):
Numer += E[i,j]*X[0,i]
Denom +=E[i,j]
mosig +=E[i,j]*(((X[0,i])-Mu[j])**2)
Mu[j] = Numer / Denom
Sigma[j]=(mosig/Denom)**0.5
pi[j]=Denom/N
def run(Sigma1,Sigma2,Mu1,Mu2,k,N,iter_num,Epsilon):
ini_data(Sigma1,Sigma2,Mu1,Mu2,k,N)
print  Mu,Sigma,pi
old=objec(k,N)
for i in range(iter_num):
e_step(k,N)
m_step(k,N)
print i,Mu,Sigma,pi
new=objec(k,N)
if abs(new-old)<2.4e-1000:
break
def objec(k,N):
global Sigma
global Mu
global E
global pi
resul=1.0
for i in xrange(0,N):
num1=0.0
for j in xrange(0,k):
num1=num1+pi[j]*E[i,j]
resul=resul*num1
print resul
return resul
if __name__ == '__main__':
run(15,8,20,70,2,1000,10,0.0001)
plt.hist(X[0,:],50)
plt.show()