动态规划(二)上机实验报告
动态规划
1、 01背包问题
2、 #include <iostream>
3、 #include <cmath>
4、 using namespace std;
5、
6、 int v_[10000][10000]; //前i个物品装入容量为j的背包中的最大价值
7、 int x[10000]; //装入背包的物品
8、
9、 int KnapSack(int w[], int v[], int n, int c){
10、 int i,j;
11、
12、 //初始化第0行和第0列
13、 for(i=0; i<=n; ++i)
14、 v_[i][0] = 0;
15、 for(j=0; j<=c; ++j)
16、 v_[0][j] = 0;
17、
18、 //计算第i行
19、 for(i=1; i<=n; ++i)
20、 for(j=1; j<=c; ++j)
21、 if(j<w[i])
22、 v_[i][j] = v_[i-1][j];
23、 else
24、 v_[i][j] = v_[i-1][j] > v_[i-1][j-w[i]]+v[i]
25、 ? v_[i-1][j] : v_[i-1][j-w[i]]+v[i];
26、
27、 //计算装入背包的物品
28、 for(j=c,i=n; i>0; --i)
29、 if(v_[i][j]>v_[i-1][j]){
30、 x[i] = 1;
31、 j = j-w[i];
32、 }else
33、 x[i] = 0;
34、
35、 //返回最大价值
36、 return v_[n][c];
37、 }
38、
39、 int main(){
40、 //w重量 v价值 n物品数 c背包容量
41、 int w[10000],v[10000];
42、 int n,c;
43、 cin>>c>>n;
44、 for(int i=1; i<=n; ++i)
45、 cin>>w[i]>>v[i];
46、 cout<<KnapSack(w,v,n,c);
47、 }
48、 最大子段和
49、 #include <iostream>
50、 #include <algorithm>
51、 using namespace std;
52、
53、 int main()
54、 {
55、 int n;
56、 int a[100000];
57、 int b[100000];
58、 cin>>n;
59、 for(int i=0; i<n; ++i){
60、 cin>>a[i];
61、 b[i] = a[i];
62、 }
63、 int max_ = 0;
64、 for(int i=0; i<n; ++i){
65、 b[i] = max(b[i],b[i-1]+a[i]);
66、 if(max_<b[i])
67、 max_ = b[i];
68、 }
69、 cout<<max_;
70、 return 0;
71、 }
72、 K-近似匹配
73、 #include <iostream>
74、 #include <cmath>
75、 #include <algorithm>
76、 using namespace std;
77、
78、 int d[10000][10000];
79、
80、 int min(int a, int b, int c){
81、 int min = a<b?a:b;
82、 if(c<min)
83、 min = c;
84、 return min;
85、 }
86、
87、 int ASM(string p, int m, string t, int n){
88、 int i,j;
89、
90、 //初始化
91、 for(j=1; j<=n; ++j)
92、 d[0][j] = j;
93、 for(i=0; i<=m; ++i)
94、 d[i][0] = i;
95、
96、 //依次计算
97、 for(j=1; j<=n; ++j)
98、 for(i=1; i<=m; ++i)
99、 if(p[i-1] == t[j-1])
100、 d[i][j] = min(d[i-1][j-1], d[i-1][j]+1, d[i][j-1]+1);
101、 else
102、 d[i][j] = min(d[i-1][j-1]+1, d[i-1][j]+1, d[i][j-1]+1);
103、
104、 //返回最小差别数
105、 return d[m][n];
106、 }
107、
108、 int main(){
109、 //p[]存储模式 t[]存储文本
110、 //char p[10000],t[10000];
111、 int m,n;
112、
113、 string p,t;
114、 cin>>p>>t;
115、 m = p.length();
116、 n = t.length();
117、
118、 // cin>>m;
119、 // for(int i=1; i<=m; ++i)
120、 // cin>>p[i];
121、
122、 // cin>>n;
123、 // for(int i=1; i<=n; ++i)
124、 // cin>>t[i];
125、
126、 cout<<ASM(p,m,t,n);
127、 return 0;
128、 }
129、 最优二叉树查找
130、 #include <iostream>
131、 #include <cmath>
132、 #include <algorithm>
133、 using namespace std;
134、
135、 int c[10000][10000];
136、
137、 int OptimalBST(int p[], int n){
138、 int i,j,k,d;
139、 int min,sum;
140、
141、 //初始化主对角线和第一条次对角线
142、 for(int i=1; i<=n; ++i){
143、 c[i][i-1] = 0;
144、 c[i][i] = p[i-1];
145、 }
146、 c[n+1][n] = 0;
147、
148、 //计算其余对角线
149、 for(d=1; d<n; ++d)
150、 for(i=1; i<=n-d; ++i){
151、 j = i+d;
152、 min = 99999777;
153、 //mink = i;
154、 sum = 0;
155、 for(k=i; k<=j; ++k){
156、 sum += p[k-1];
157、 if(c[i][k-1]+c[k+1][j]<min){
158、 min = c[i][k-1]+c[k+1][j];
159、 }
160、 }
161、 c[i][j] = min+sum;
162、 }
163、
164、 ////////////////////////////
165、 // for(i=0; i<=n; ++i){
166、 // for(j=0; j<=n; ++j)
167、 // cout<<c[i][j]<<"\t";
168、 // cout<<endl;
169、 // }
170、
171、 return c[1][n];
172、 }
173、
174、 int main(){
175、 //n个字符的查找概率存储在p[]中
176、 int p[10000];
177、 int n;
178、
179、 cin>>n;
180、 int del=0;
181、 for(int i=0; i<n; ++i){
182、 cin>>p[i];
183、 del+=p[i];
184、 }
185、
186、 cout<<OptimalBST(p,n)-del;
187、 }
四、运行输出结果:
1、 01背包问题
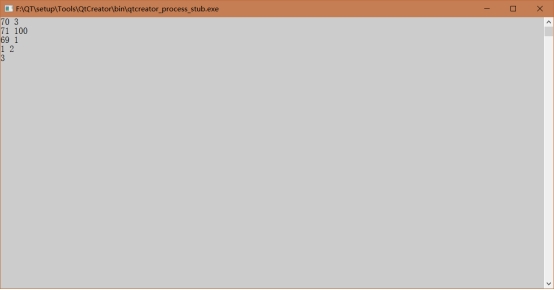
2、 最大子段和
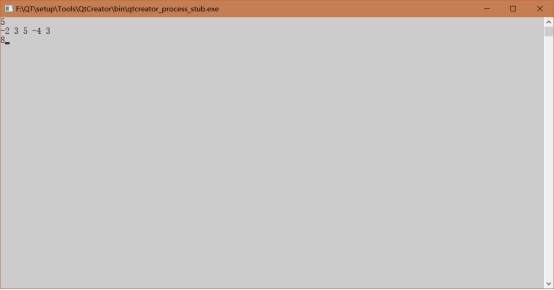
3、 K-近似匹配
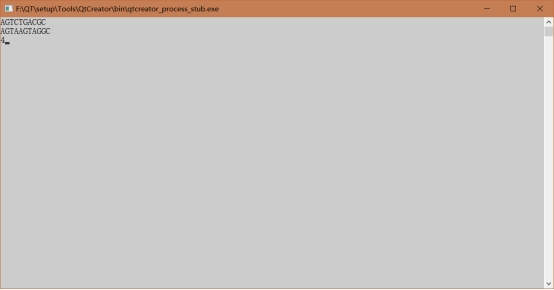
4、 最优二叉树查找
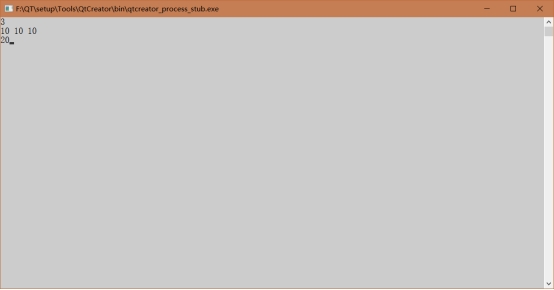
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训:
1、我一开始把二叉查找树那里的一些数据类型搞错了,导致出现了一些错误(数据类型不匹配)。
2、最优二叉树查找里面我没有将double改成int导致结果出错了,这个低级错误耗了我好长好长时间QAQ。

