《算法设计与分析-动态规划》实验报告
一、实验内容:
动态规划问题。
手算内容:
TSP问题

二、所用算法的基本思想及复杂度分析:
1、 数塔问题
1) 基本思想
假设一个n层的数塔,从顶端的数开始,要想求最大数值和,只要该点求其下面一层两个数塔中最大数值和更大的那个,如此循环直到最后一层选数值最大的那个。
2) 复杂度分析
存放每一步决策的数组最后一层赋值为数塔最后一层的复杂度为O(n);求每一步决策的最大数值和的复杂度为O(n2),所以总复杂度为O(n2)。
2、 多段图最短路径
1) 基本思想
将多端图分为k段,从第1个顶点开始不断查找其可达的顶点到达最后一个点的最短路径,如此循环直到找到最短路径。
2) 复杂度分析
先是计算第一个顶点到各个点的最短路径,需要两层循环,外层循环n-1次,内层循环所有入边,假设点数为v_num,则复杂度为O(v_num);假设分为k段,则输出的复杂度为O(k),总复杂度为O(v_num+k)。
3、 最长递增子序列
1) 基本思想
记录每一个数的最长子序列,如果后续数大于这个数,则后续数的最长子序列长度+1,并且在原有子序列基础上加入这个后续数。如此反复,最终获得每个数的最长递增子序列。
2) 复杂度分析
寻找最长子序列需要两层循环,外层循环n-1次,内层循环循环所有该点之前的点,而在这个内层循环中为了记录更新后的最长子序列,又需要一个循环,总的时间复杂度为O(n2)。
三、源程序及注释:
1、 数塔问题
2、 #include <iostream>
3、 using namespace std;
4、 int d[10000][10000] = {0}; //数塔
5、 int maxAdd[10000][10000] = {0}; //存储动态规划的每一步决策结果
6、 int path[10000][10000] = {0}; //存放选择的路径
7、
8、 int dataTower(int n){
9、 int i,j;
10、 //将底层数塔值赋给底层maxAdd
11、 for(j=0; j<n; ++j){
12、 maxAdd[n-1][j] = d[n-1][j];
13、 }
14、 //从倒数第二层开始一层一层往上求最大子数塔最大数值和
15、 for(i=n-2; i>=0; --i)
16、 for(j=0; j<=i; ++j)
17、 //如果左侧子数塔大,则选左侧子数塔
18、 if(maxAdd[i+1][j] > maxAdd[i+1][j+1]){
19、 maxAdd[i][j] = d[i][j] + maxAdd[i+1][j];
20、 path[i][j] = j;
21、 }else{
22、 //如果右侧子数塔大,则选右侧子数塔
23、 maxAdd[i][j] = d[i][j] + maxAdd[i+1][j+1];
24、 path[i][j] = j+1;
25、 }
26、 //输出
27、 cout<<"路径为:"<<d[0][0];
28、 j = path[0][0];
29、 for(i=1; i<n; ++i){
30、 cout<<"-->"<<d[i][j];
31、 j = path[i][j];
32、 }
33、 cout<<endl;
34、 //返回最大数值和
35、 return maxAdd[0][0];
36、 }
37、
38、
39、 int main()
40、 {
41、 //层数
42、 int n;
43、 cin>>n;
44、 for(int i=0; i<n; ++i)
45、 for(int j=0; j<=i; ++j)
46、 cin>>d[i][j];
47、 cout<<dataTower(n);
48、 }
49、 多段图最短路径
50、 #include <iostream>
51、
52、 using namespace std;
53、 const int MAX = 1000;
54、 int arc[10000][10000]; //代价矩阵,即点i到点j的权值
55、 int cost[10000]; //路劲长度
56、 int path[10000]; //路径
57、
58、 //创建代价矩阵
59、 int createGraph(){
60、 int i,j,k;
61、 int weight;
62、 int v_num,arc_num;
63、 cin>>v_num>>arc_num;
64、 //初始化代价矩阵设置值为无穷大,即MAX,表示不可达。
65、 for(i=0; i<v_num; ++i)
66、 for(j=0; j<v_num; ++j)
67、 arc[i][j] = MAX;
68、 //更新代价矩阵
69、 for(k=0; k<arc_num; ++k){
70、 //输入边的两个顶点和权值
71、 cin>>i>>j>>weight;
72、 arc[i][j] = weight;
73、 }
74、 return v_num;
75、 }
76、
77、 //求最短路径
78、 int minPath(int n){
79、 int i,j;
80、 //初始化路径长度为不可达,即max
81、 //初始化路径为-1
82、 for(i=1; i<n; ++i){
83、 cost[i] = MAX;
84、 path[i] = -1;
85、 }
86、 //设置第一个顶点
87、 cost[0] = 0;
88、 path[0] = -1;
89、 //从第二个顶点开始不断查找最短路径并记录
90、 for(j=1; j<n; ++j)
91、 for(i=j-1; i>=0; --i){
92、 if(arc[i][j] + cost[i] < cost[j]){
93、 cost[j] = arc[i][j] + cost[i];
94、 path[j] = i;
95、 }
96、 }
97、 //输出
98、 cout<<n-1;
99、 i = n-1;
100、 while(path[i] >= 0){
101、 cout<<"<-"<<path[i];
102、 i = path[i];
103、 }
104、 cout<<endl;
105、 return cost[n-1];
106、 }
107、
108、 int main()
109、 {
110、 cout<<minPath(createGraph());
111、 }
112、 最长递增子序列
113、 #include <iostream>
114、
115、 using namespace std;
116、
117、 int L[100]; //L[i]数组存数a[i]的最长递增子序列长度
118、 int x[100][100]; //x[i]数组存到a[i]为止的最长递增子序列
119、
120、 int maxIncreaseOrder(int a[], int n){
121、 int i,j,k,index;
122、 //初始化L和x
123、 for(i=0; i<n; ++i){
124、 L[i] = 1;
125、 x[i][0] = a[i];
126、 }
127、 //寻找最长子序列并记录
128、 for(i=1; i<n; ++i){
129、 int max = 1;
130、 for(j=i-1; j>=0; --j){
131、 if(a[j]<a[i] && max<L[j]+1){
132、 max = L[j]+1;
133、 L[i] = max; //更新L
134、 //更新x
135、 for(k=0; k<max-1; ++k)
136、 x[i][k] = x[j][k];
137、 x[i][max-1] = a[i];
138、 }
139、 }
140、 }
141、 //查找最长子序列的最终点位置
142、 for(index=0,i=1; i<n; ++i)
143、 if(L[index]<L[i])
144、 index = i;
145、 //输出
146、 for(i=0; i<L[index]; ++i)
147、 cout<<x[index][i]<<" ";
148、 cout<<endl;
149、 //返回长度
150、 return L[index];
151、 }
152、
153、 int main()
154、 {
155、 int n,a[100];
156、 cin>>n;
157、 for(int i=0; i<n; ++i)
158、 cin>>a[i];
159、 cout<<maxIncreaseOrder(a,n);
160、 }
四、运行输出结果:
1、 数塔问题
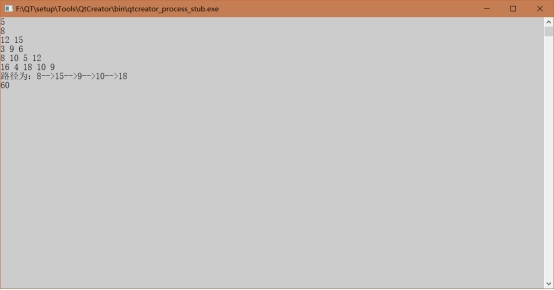
2、 多段图最短路径
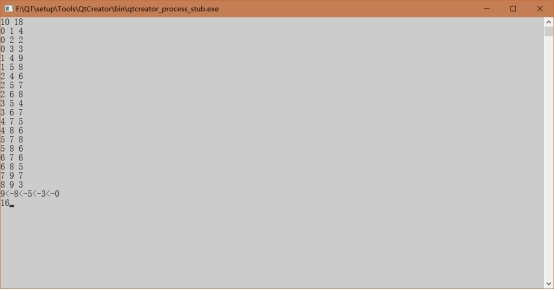
3、 最长递增子序列
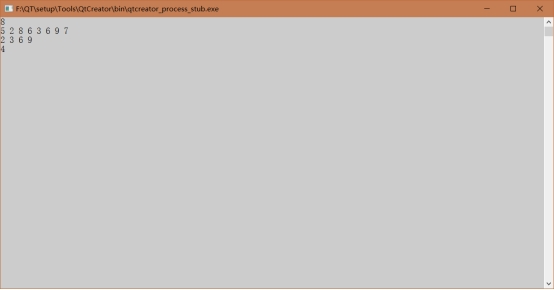
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训:
1、关于这个最长递增子序列问题,答案可能是不唯一的。所以可以改进一下,通过链表来存放所有最长递增子序列。书上采用的是数组的方式,造成的结果就是无法存放所有答案。

