《算法设计与分析-回溯法》上机实验报告
eograph;">252、 int sum = 0;
253、 while (!q.empty()){
254、 n1 = q.front();
255、 q.pop();
256、 sum++;
257、 for (int i = 0; i < 4; i++){
258、 int xtmp = n1.x + direction[i].dx;
259、 int ytmp = n1.y + direction[i].dy;
260、 //符合要求且颜色相同
261、 if (judge(xtmp, ytmp) && color[xtmp][ytmp] == color[x][y]){
262、 node n2;
263、 n2.x = xtmp;
264、 n2.y = ytmp;
265、 q.push(n2);
266、 visited[xtmp][ytmp] = true;
267、 }
268、 }
269、 }
270、 return sum;
271、 }
272、
273、 int main()
274、 {
275、 initDirection();
276、 while(cin>>m>>n){
277、 //访问初始化
278、 memset(visited, false, sizeof(visited));
279、 for(int i=0; i<m; ++i)
280、 cin >> color[i];
281、 int maxSum = 0;
282、 for(int i=0; i<m; ++i){
283、 for(int j=0; j<n; ++j){
284、 maxSum = max(maxSum,bfs(i,j));
285、 }
286、 }
287、 cout<<maxSum<<endl;
288、 }
289、 return 0;
290、 }
四、运行输出结果:
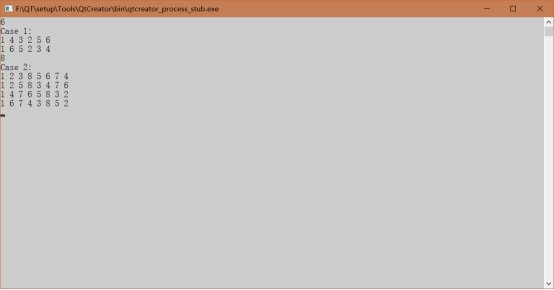
1、 素数环--1789
2、 八皇后--1058
3、 迷宫问题--1165
4、 魔方问题--1061
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训:
1、素数环问题,一直显示超时,后来经过老师提醒,判断如果奇数则跳过后AC了。
2、八皇后问题,输出顺序老是不对,后来发现原来题目中输出时将i和j顺序互换了。
3、迷宫问题发现了昨天的错误,是判断超过边界的判断式有问题,不过这次我仍然用的加边框的方式过的。
, 一、实验内容:
回溯法问题。
二、所用算法的基本思想及复杂度分析:
1、 素数环--1789
1) 基本思想
对于第一个点,固定为1,剩下的点我们从2开始不断试探,如果不满足条件(和前一个点相加不为素数或者重复)则回溯。
PS:最后一个点和第一个点相加
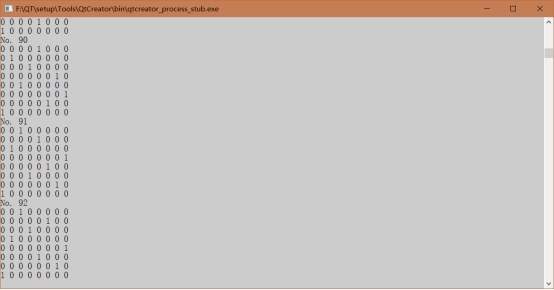
2、 八皇后--1058
1) 基本思想
首先对于每一行,先从第一列开始放置,如果不行(竖线和对角有其他皇后)换下一个个位置,可以的话换下一行。如果有一行的皇后无法摆放就回溯。要是所有都试过了仍然有皇后没有摆放位置,则无解。
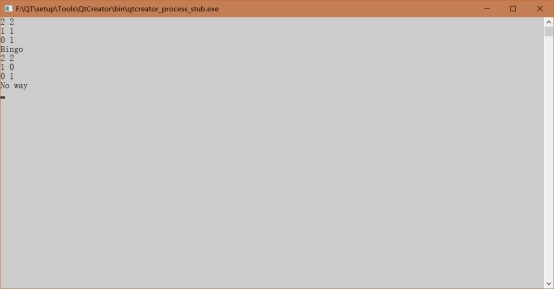
3、 迷宫问题--1165
1) 基本思想
首先从起点出发,搜索8个方向,如果通且未访问过则继续,并标记已访问,如果不通已访问则试探下一个点,如果都不行则回溯。这里在外层全套上0,即加入不可通的边框。
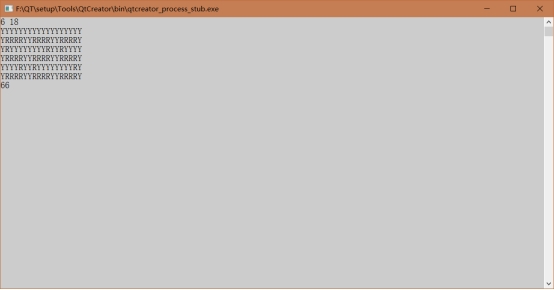
4、 魔方问题--1061
1) 基本思想
其实非常类似迷宫问题,上下左右四个方向进行搜寻,如果访问过就标记下,没有了或者全部访问过了则返回,对于输入的每一个颜色重复上述操作,如果有更大的便更新最大色块来找到最大的那个色块。
三、源程序及注释:
1、 素数环--1789
2、 #include <iostream>
3、 #include <cmath>
4、 using namespace std;
5、
6、 int a[21] = {0}; //数
7、 int n;
8、
9、 //判断是否是素数
10、 bool isPrime(int tmp){
11、 for(int i=2; i<=sqrt(tmp); ++i)
12、 if(tmp % i == 0)
13、 return 0;
14、 return 1;
15、 }
16、
17、 //判断素数是否重复
18、 bool judge(int k){
19、 bool flag = 0;
20、 //重复则返回0
21、 for(int i=0; i<k; ++i)
22、 if(a[i]==a[k])
23、 return 0;
24、 flag = isPrime(a[k]+a[k-1]);
25、 //最后一个数和第一个数
26、 if(flag==1 && k==n-1)
27、 flag = isPrime(a[k]+a[0]);
28、 return flag;
29、 }
30、
31、 void primeCircle(int n){
32、 //初始化数组
33、 for(int i=0; i<n; ++i){
34、 a[i] = 0;
35、 }
36、 int k=1; //下标
37、 a[0] = 1; //初始化为第一个数
38、 while(k>=1){
39、 a[k] += 1; //取下一个数
40、 //判断重复就取别的数
41、 while(a[k]<=n){
42、 if(judge(k))
43、 break;
44、 else
45、 a[k] += 1;
46、 }
47、 //输出
48、 if(a[k]<=n && k==n-1){
49、 for(int i=0; i<n-1; ++i)
50、 cout<<a[i]<<" ";
51、 cout<<a[n-1]<<endl;
52、 }
53、 //处理下个顶点
54、 if(a[k]<=n && k<n-1)
55、 k += 1;
56、 else
57、 a[k--] = 0; //回溯
58、 }
59、 }
60、
61、 int main()
62、 {
63、 int count = 0;
64、 while(cin>>n){
65、 count++;
66、 cout<<"Case "<<count<<":"<<endl;
67、 if(n==1)
68、 cout<<1<<endl;
69、 if(n%2==1)
70、 continue;
71、 primeCircle(n);
72、 }
73、 return 0;
74、 }
75、 八皇后--1058
76、 #include <iostream>
77、 #include <cmath>
78、 using namespace std;
79、
80、 int x[100]={0}; //第i个皇后摆放在第i行第i个位置
81、 int count = 0; //记录有几个解
82、
83、 //看皇后k放在x[k]会不会冲突
84、 bool judge(int k){
85、 for(int i=0; i<k; ++i)
86、 if(x[i]==x[k] || abs(i-k)==abs(x[i]-x[k]))
87、 return 1;
88、 return 0;
89、 }
90、
91、 void Queen(int n){
92、 for(int i=0; i<n; ++i)
93、 x[i] = -1;
94、 int k=0;
95、 while(k>=0){
96、 x[k]++; //在下一列放皇后k
97、 //冲突处理
98、 while(x[k]<n && judge(k)==1)
99、 x[k]++; //试探下一个位置
100、 //输出一个解
101、 if(x[k]<n && k==n-1){
102、 count++;
103、 cout<<"No. "<<count<<endl;
104、 for(int i=0; i<n; ++i){
105、 for(int j=0; j<n; ++j)
106、 cout<<(i==x[j])<<" ";
107、 cout<<endl;
108、 }
109、 }
110、 //有皇后未摆放
111、 else if(x[k]<n && k<n-1)
112、 k++; //准备摆放
113、 else
114、 x[k--] = -1; //回溯,重放皇后k
115、 }
116、 }
117、
118、 int main()
119、 {
120、 // int n;
121、 // cin>>n;
122、 Queen(8);
123、 //cout<<"共"<<count<<"个解";
124、 return 0;
125、 }
126、 迷宫问题--1165
127、 #include <iostream>
128、 using namespace std;
129、
130、 int xIn, yIn, xOut, yOut; //出入口坐标
131、 int xLength, yLength; //迷宫的行数和列数
132、 int maze[1000][1000]; //迷宫数组
133、 bool visited[1000][1000] = {0}; //访问标记数组
134、
135、 struct direction{
136、 int dx, dy;
137、 void setDirection(int dx,int dy){
138、 this->dx = dx;
139、 this->dy = dy;
140、 }
141、 }direction[4];
142、
143、 void initDirection(){
144、 direction[0].setDirection(0,1); //东
145、 direction[1].setDirection(1,0); //南
146、 direction[2].setDirection(0,-1); //西
147、 direction[3].setDirection(-1,0); //北
148、 }
149、
150、 //解决迷宫问题的递归算法
151、 bool seekPath(int x, int y){
152、 //从迷宫某一位置[i][j]开始,寻找出口[xOut][yOut]的一条路径,如果找到,则函数返回true
153、 int xtmp, ytmp; //记录位置信息
154、 if(x==xOut && y==yOut)
155、 return true;
156、 //循环遍历(x,y)的8个方向
157、 for(int i=0; i<4; i++) {
158、 xtmp = x+direction[i].dx;
159、 ytmp = y+direction[i].dy;
160、
161、 // if(xtmp<0 || xtmp>=xLength || ytmp<0 || ytmp>=yLength)
162、 // continue;
163、
164、 //找下一位置寻找通向出口的路径
165、 if(maze[xtmp][ytmp]==1 && visited[xtmp][ytmp]==0){ //如果通且未被访问过
166、 visited[xtmp][ytmp] = 1; //标记为已访问过
167、 if(seekPath(xtmp, ytmp)){ //递归试探
168、 // printf("(%d,%d)\n",xtmp-1,ytmp-1);//逆向输出路径坐标
169、 return true;
170、 }
171、 }
172、 //回溯,换一个方向再试探通向出口的路径
173、 }
174、 return false; //找不到通向出口的路径
175、 }
176、
177、 int main(){
178、 initDirection(); //初始化方向
179、 while(cin>>xLength>>yLength){
180、 for(int i=0; i<=yLength+1; ++i){
181、 maze[0][i] = 0;
182、 maze[xLength+1][i] = 0;
183、 }
184、 for(int i=0; i<=xLength+1; ++i){
185、 maze[i][0] = 0;
186、 maze[i][yLength+1] = 0;
187、 }
188、 for(int i = 1; i <= xLength; i++)
189、 for(int j = 1; j <= yLength; j++) {
190、 cin >> maze[i][j];
191、 visited[i][j] = 0;
192、 }
193、 xIn = 1;
194、 yIn = 1;
195、 xOut = xLength;
196、 yOut = yLength;
197、 visited[xIn][yIn] = 1; //从入口开始
198、 if(seekPath(xIn, yIn))
199、 cout<<"Bingo";
200、 else
201、 cout<<"No way";
202、 cout<<endl;
203、 }
204、 return 0;
205、 }
206、 魔方问题--1061
207、 #include <iostream>
208、 #include <cmath>
209、 #include <queue>
210、 #include <cstring>
211、 using namespace std;
212、
213、 char color[100][100];
214、 bool visited[100][100];
215、 int m, n; //魔方的行、列
216、
217、 struct direction{
218、 int dx, dy;
219、 void setDirection(int dx,int dy){
220、 this->dx = dx;
221、 this->dy = dy;
222、 }
223、 }direction[4];
224、
225、 void initDirection(){
226、 direction[0].setDirection(0,1); //东
227、 direction[1].setDirection(1,0); //南
228、 direction[2].setDirection(0,-1); //西
229、 direction[3].setDirection(-1,0); //北
230、 }
231、
232、 struct node{
233、 int x, y;
234、 };
235、
236、 bool judge(int x, int y){
237、 if(x>=0 && x<m && y>=0 && y<n && visited[x][y]==0)
238、 return 1;
239、 return 0;
240、 }
241、
242、 int bfs(int x, int y){
243、 if (visited[x][y] == 1){
244、 return 0;
245、 }
246、 queue<node> q;
247、 node n1;
248、 n1.x = x;
249、 n1.y = y;
250、 q.push(n1);
251、 visited[x][y] = 1;
全套毕业设计论文现成成品资料请咨询

