sfa与生产函数

（一）SFA模型
面板随机边界模型：包括效率不随时间变化的panel-SFA模型，效率随时间变化的panel-SFA模型，TFE-SFA模型、缩放因子模型、以及动态SFA模型。
各模型的设定特点如下：




模型


特点




1、效率不随时间变化


所有不随时间变化的个体因素都归入了非效率项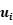




随机效应RE


无效率项为随机变量，局限在于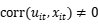




固定效应FE


无效率项为固定效应，效率采用相对值，局限在于u不随时间变动，且估计有偏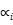（包含所有不随t变化的变量）




2、效率随时间变化


允许无效率项随时间变化，但假设在同一年度上，所有公司非效率项的变化模式都相同，从本质上讲也是把个体因素归入非效率项




CSS90&LS93


CSS90将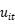设定为t的二次函数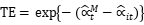，，局限在于参数过多；而LS93虽然将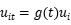,但灵活性相对降低，意味着同一年度上所有个体的效率相同。




Kumb90时变SFA


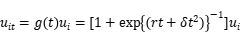要检验技术效率是否随时间变化，只需设定原假设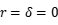




BC92 时间衰减SFA


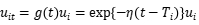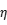，称为延迟参数，用以衡量非效率项随时间的下降程度，对于公司而言，最后一期的非效率程度即为该公司非效率程度的比较基准




3、TFE-SFA


Greene难题：无法区分个体异质性与无效率成分（对于SF的不当设定会导致TE估计值的有偏）；解决方法1：产出函数中加入个体效应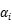以反映个体异质性，进而使用极大似然估计法强行估计参数，但容易造成参数冗余而无法收敛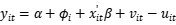，,，x中不能包含不随时间变化的因素，否则会与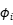共线性




TRE


把个体效应视为随机变量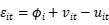,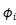是个体效应，需要假设其与解释变量x不相关，但x可以包含不随时间变化的因素




G-TRE


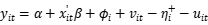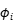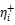一般化模型，应用三步估计法。，模型的复合干扰项包括四项，衡量那些不随时间变化的个体效应(个体异质性),衡量一般意义上的随机干扰，捕捉长期无效率因素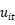，反应短期无效率因素；局限：仍然是随机效应模型，需假设四项干扰项iid彼此独立，与x不相关。




4、缩放因子模型


组内差分/一阶差分去除个体效应，需要使用蒙特卡罗模拟进行参数估计（边际极大似然估计法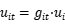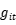），是影响

      非效率的外生变量 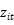的函数，允许异质性及时序连续性




5、动态SFA模型


使干扰项可以自相关，更切合实际




动态sfa模型设定：







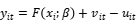
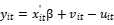
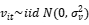
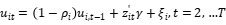
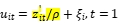
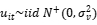
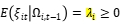
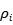衡量第i家公司对非效率项的调整能力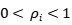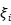（）,为非负的干扰项,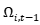表示在第t-1期能够获得的所有信息集。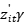控制了影响非效率的外生变量（选取什么作为外生变量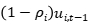？），为不可观测到的因素导致的非效率留存。在第t期期初，公司了解到上期无效率水平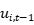（）并采取措施改善了部分无效率。
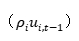想法：如果要做不同类型模型的对比，可以用G-TRE、缩放因子模型加上动态SFA来做非效率项估计的对比。
估计方法：
sftpe用的是MCMC估计
sfpanel针对不同类型用到的估计方法不同


（二）产出/成本函数设定 参照(何东伟 et al., 2017)的设定。用因子变量写法来表示模型中的交乘项。参见 help fvvarlist以及 「因子变量简介」。

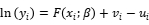
其中F是生产函数的形式，在做随机前沿分析时最常用的生产函数形式是Cobb-Douglas生产函数和Translog生产函数，Cobb-Douglas生产函数要求所有样本单元的规模报酬均相同，而Translog生产函数是CD函数更一般的形式，因此采用Translog函数设定成本/利润函数。

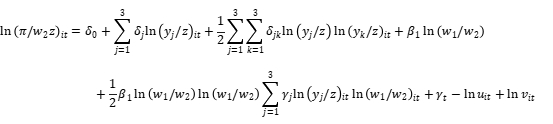
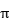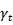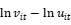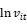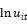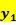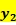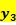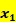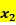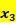其中，i和t分别代表银行和时间，代表银行的利润。利润函数中包含三个产出变量：总存款y1、总贷款y2和其他盈利性资产y3；两个投入变量：资金成本w1和劳动力成本w2。我们在随机前沿函数中加入了年份虚拟变量，进而控制住年份固定效应。是综合误差项，其中是随机误差项，是无效率项。（想法：产出变量――扣除不良贷款后的贷款 存款和短期基金 其他盈利资产；投入变量――可贷资金 劳动力和固定资产投入 权益资本 (待定)）
在函数方程中，我们用银行的总资产z对变量进行标准化，从而减少了异方差并且使得不同规模的银行的残差项具有可比性。同时用劳动力成本w2进行标准化，进而保证价格同质性（这点与(Tsionas, 2010)将总成本和所有价格都基于w5标准化了的想法一致）。在估计中，一些财务指标为负数，无法直接取对数，因此，我们在这些指标统一加入常数项，得到正的数值。除了利润函数和成本函数的效率以外，我们还估计了利息收入效率。
(谭政勋 and 李丽芳, 2016) 如果单纯地使用各银行自身的要素费用除以全部要素投入来得到各要素价格会使得要素投入的价格具有很强的内生性（Patti and Hardy( 2005) 、姚树洁等( 2011) ），导致变量设定违背成本和利润函数中假设要素投入的价格是外生的假设条件。因此，借鉴其做法，将模型中的设定为市场平均投入要素的价格，即被测算银行以外的其他银行要素投入价格的平均值。
Tsionas, E.G., 2010, Inference in dynamic stochastic frontier models. Journal of Applied Econometrics 21, 669-676.
何东伟, 王春英, 胥莉, 2017, 地理扩张、行政级别与中小银行绩效. 上海金融, 38-44.
谭政勋, 李丽芳, 2016, 中国商业银行的风险承担与效率――货币政策视角. 金融研究, 112-126.