目录
1.三种差值方法的实现与问题	
2. 随机丢点的评估	
1.三种差值方法的实现与问题	
三种插值方法都是使用Python自己实现的。	
3.1 最近邻插值	
3.3 径向基函数插值	
2. 随机丢点的评估	
2.1 肉眼观察	
2.2 指标变化曲线	
2.2.1 三种算法比较	
2.2.2 RBF三种基函数比较	
3.涂鸦、写字等破坏的评估	
3.1 结果展示	
3.2 指标得分	
3.3 极限测试	
4. 总结	
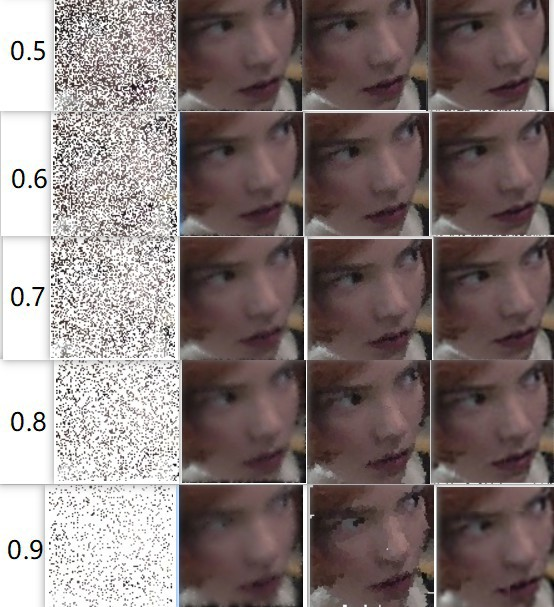
1.三种差值方法的实现与问题
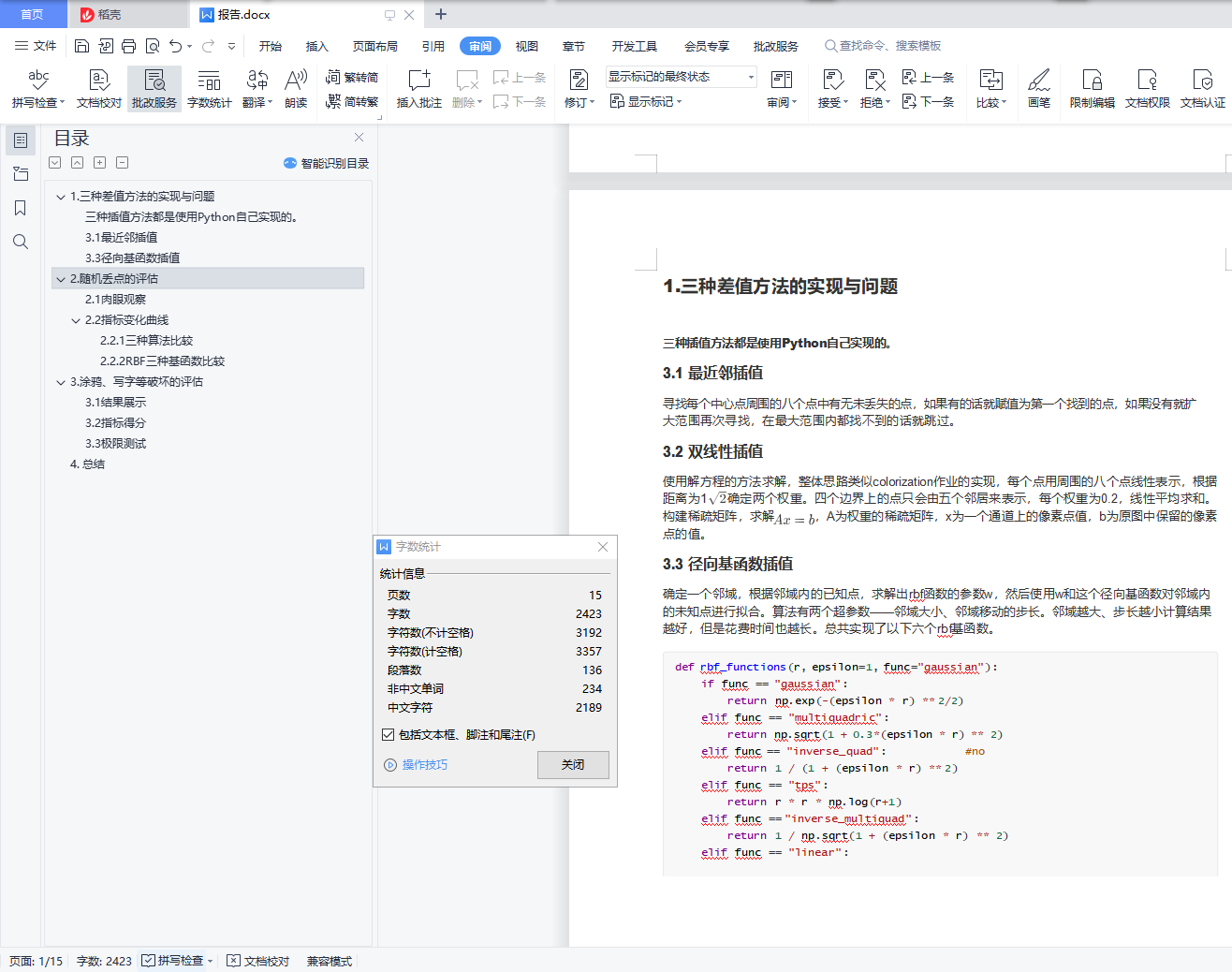
三种插值方法都是使用Python自己实现的。
3.1 最近邻插值
寻找每个中心点周围的八个点中有无未丢失的点，如果有的话就赋值为第一个找到的点，如果没有就扩 大范围再次寻找，在最大范围内都找不到的话就跳过。
3.2 双线性插值
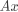
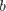使用解方程的方法求解，整体思路类似colorization作业的实现，每个点用周围的八个点线性表示，根据   距离为1 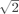确定两个权重。四个边界上的点只会由五个邻居来表示，每个权重为0.2，线性平均求和。    构建稀疏矩阵，求解	，A为权重的稀疏矩阵，x为一个通道上的像素点值，b为原图中保留的像素 点的值。
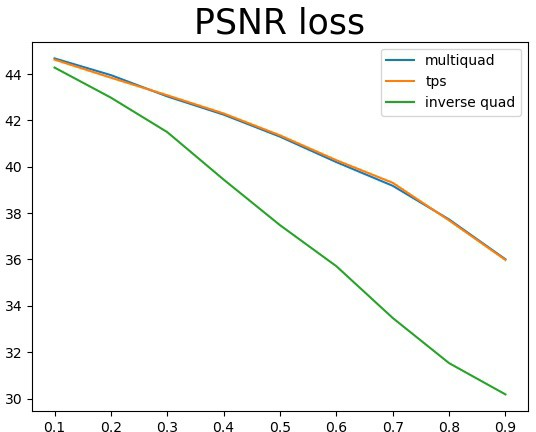
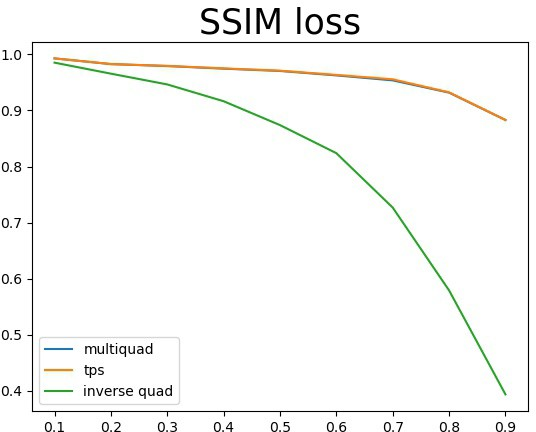
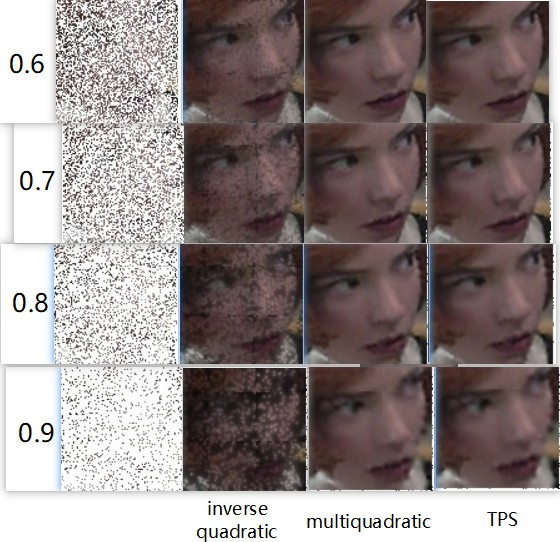
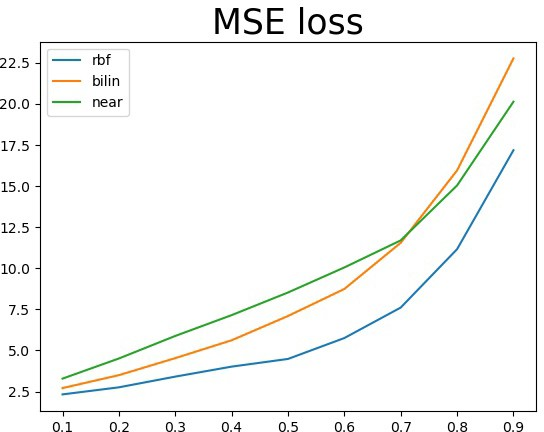
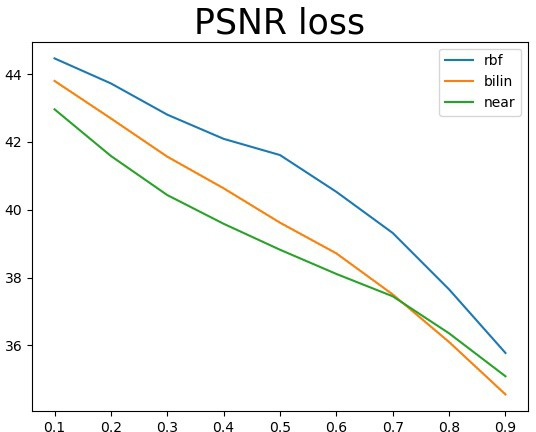
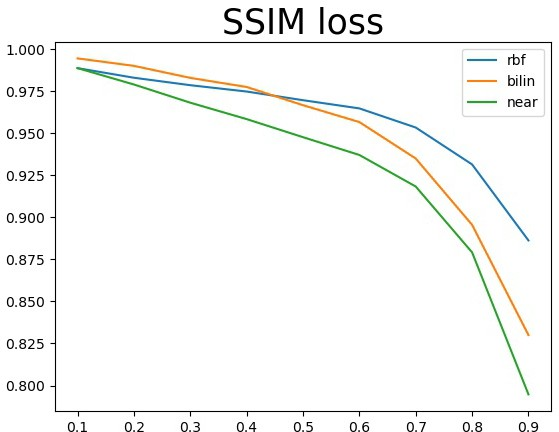
3.3 径向基函数插值
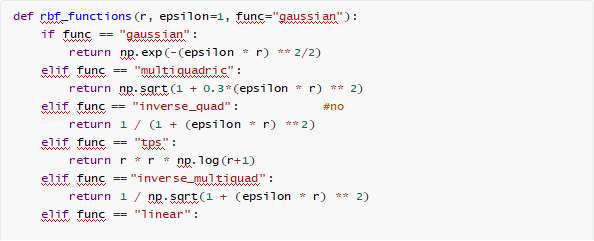
确定一个邻域，根据邻域内的已知点，求解出rbf函数的参数w，然后使用w和这个径向基函数对邻域内   的未知点进行拟合。算法有两个超参数――邻域大小、邻域移动的步长。邻域越大、步长越小计算结果 越好，但是花费时间也越长。总共实现了以下六个rbf基函数。