目录
1. 给出过约束线性系统解的推导	
2. 给出	的解的数学解释	
3.染色算法的评估	
3.1 实现原理	
3.2 染色结果	
失败的涂鸦与染色效果	
3.3 算法的其他测试	
3.4 优缺点总结	
1. 给出过约束线性系统解的推导



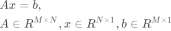
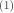
因为A不是满秩方阵，所以不能直接得出	，使用最小二乘法计算x的值，
.
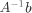
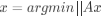
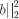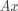
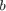
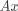
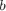令	, 则




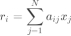
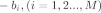
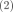
误差的平方和为




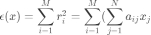
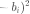
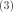
带入r的向量化表示	到(3)，则(3)可以改写为向量形式： 为了最小化误差 ，需要对其求x的偏导：



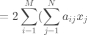
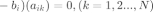
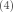
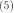
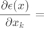
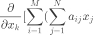
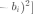可以化简为：



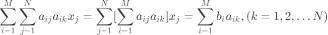
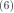
(6)的向量形式为：



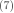
所以，	。
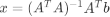
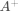
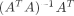
因为A列满秩，所以广义逆	，即	。



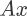
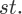
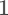
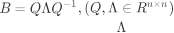
2. 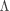给出	的解的数学解释




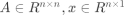
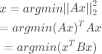
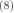
将矩阵B做特征值分解，得到	，Q是正交特征向量组成的矩阵， 是特征值(由大到小排列)组成的对角矩阵，问题的解就是 中最小非零解对应的特征向量。
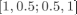
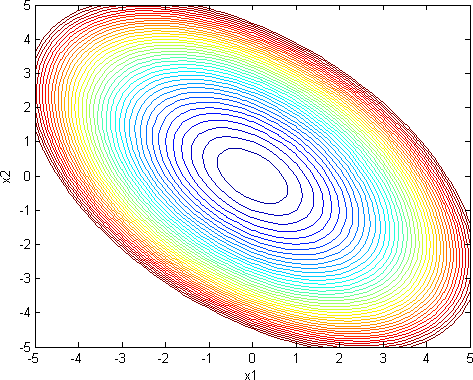
假 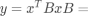                           ,则y的等高线图	如下：


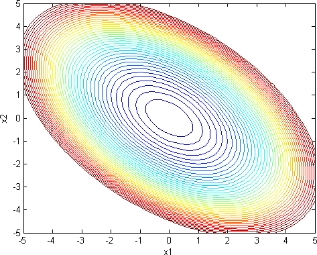
可以看出如果在x=1的约束下，也就是一个原点为中心的圆形，这个圆形与等高线交点中y的最小值恰好 是较小特征向量的位置[-0.7071;0.7071]，也是等高线变化最稀疏的位置。如果将维度推广到三维时，
x=1的约束变为一个球形，对应的解是椭球与球形的短轴交点。对应的推广到三维以上时，与三维的结 果也类似。