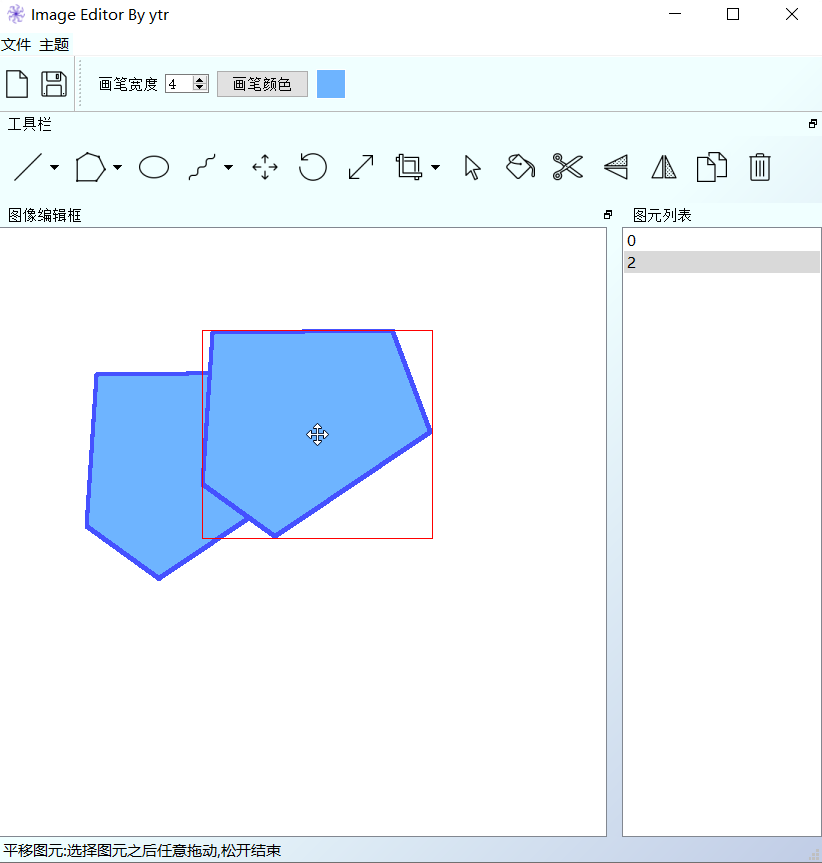
基于Python实现的图形绘制系统 课程论文+项目源码+系统说明书+演示视频
目录
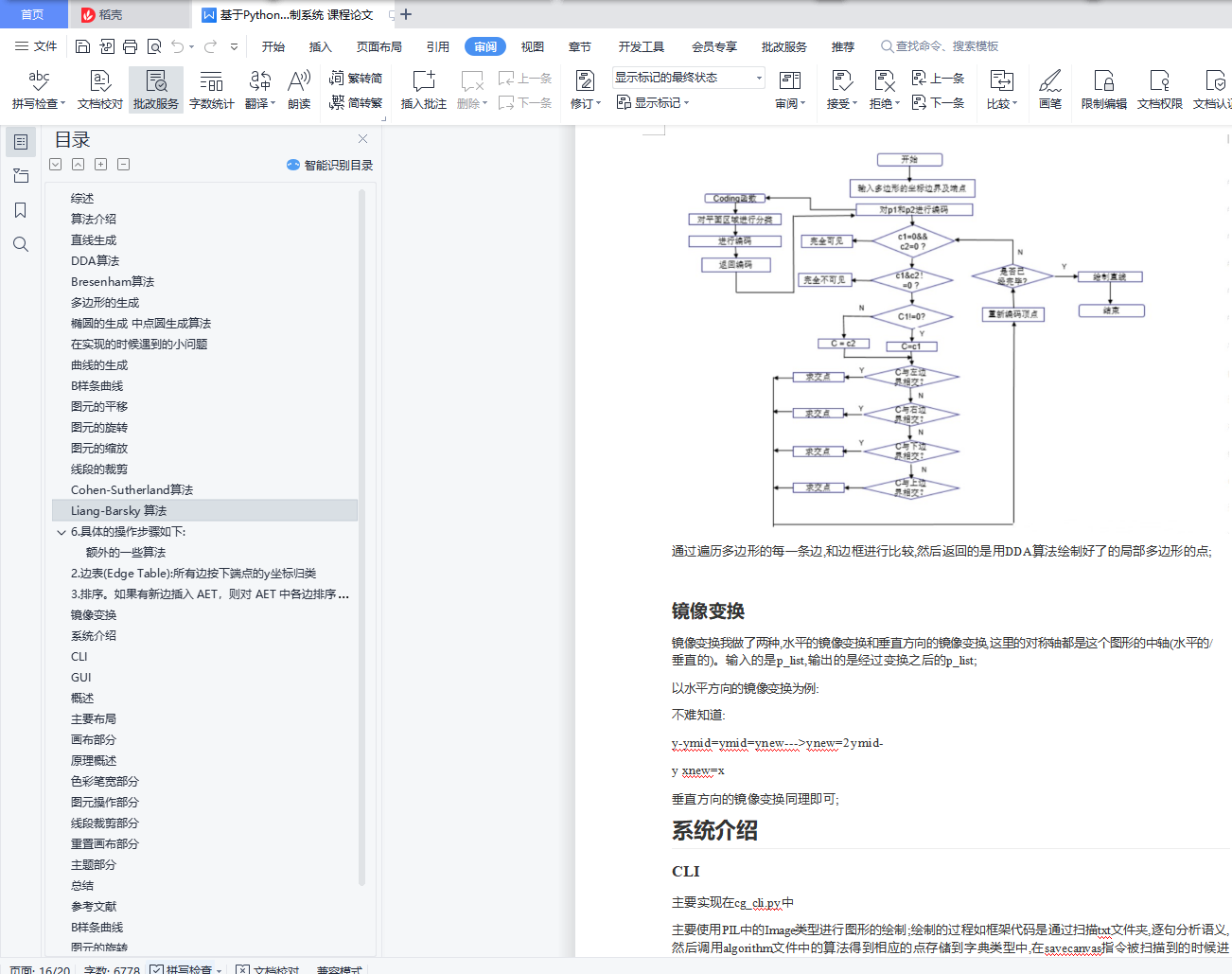
2. 边表(Edge Table):所有边按下端点的y坐标归类
3. 排序。如果有新边插入 AET,则对 AET 中各边排序;
综述
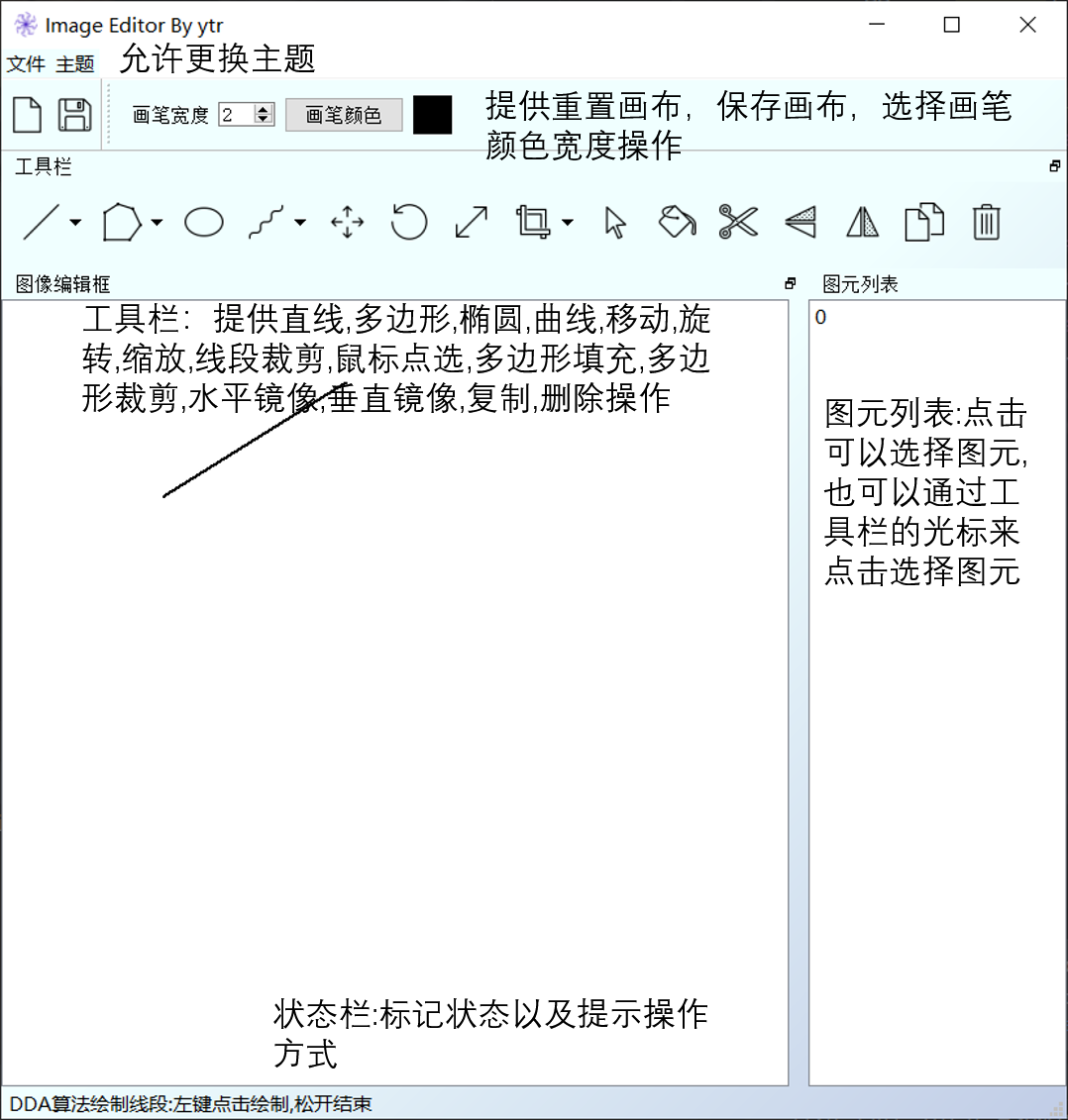
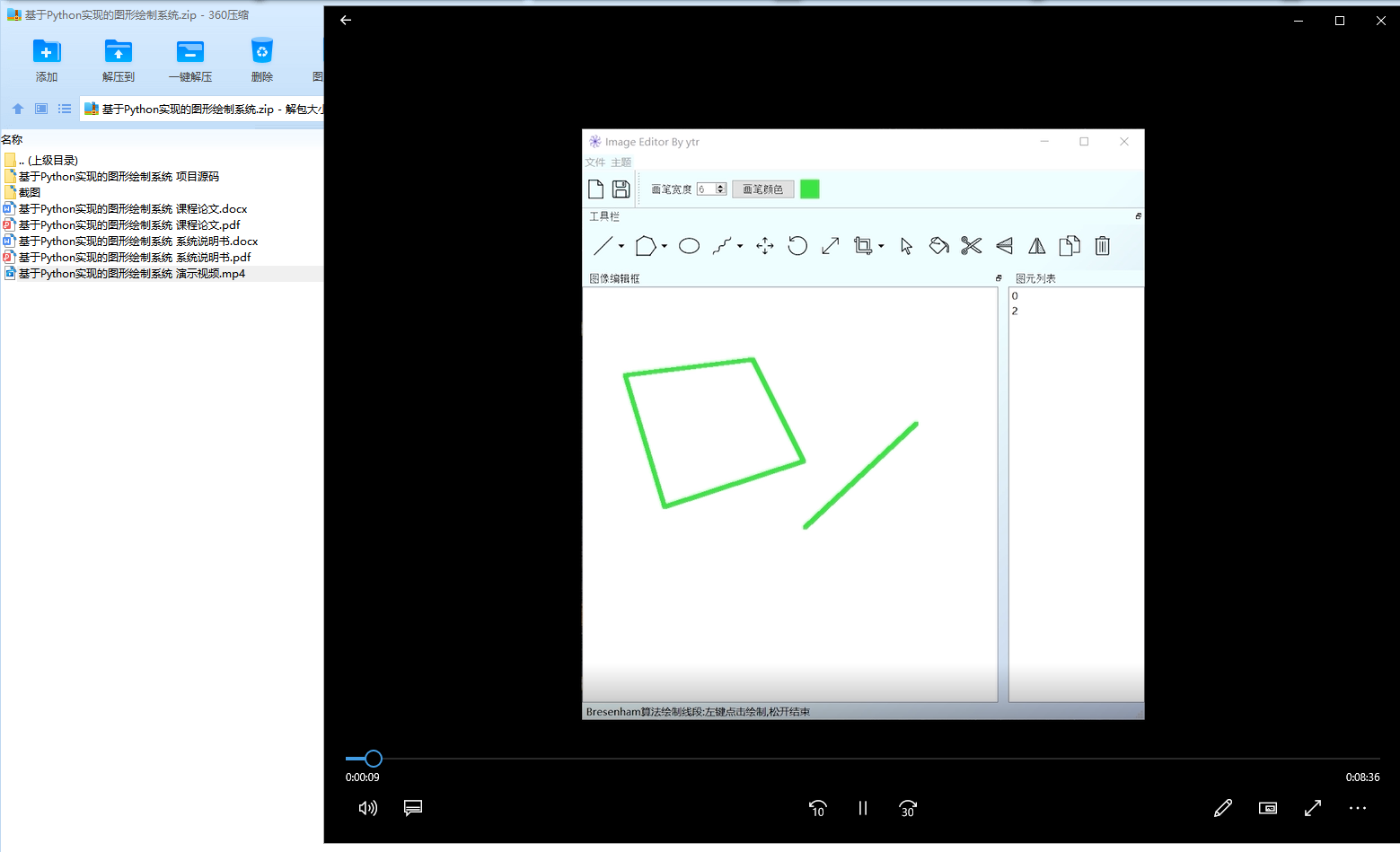
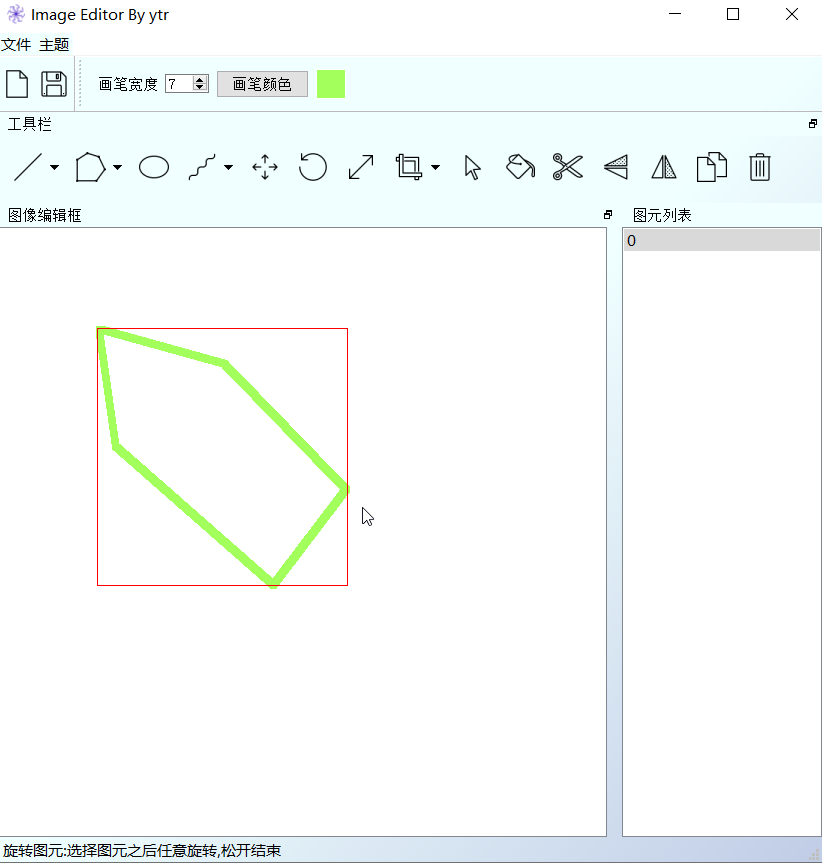
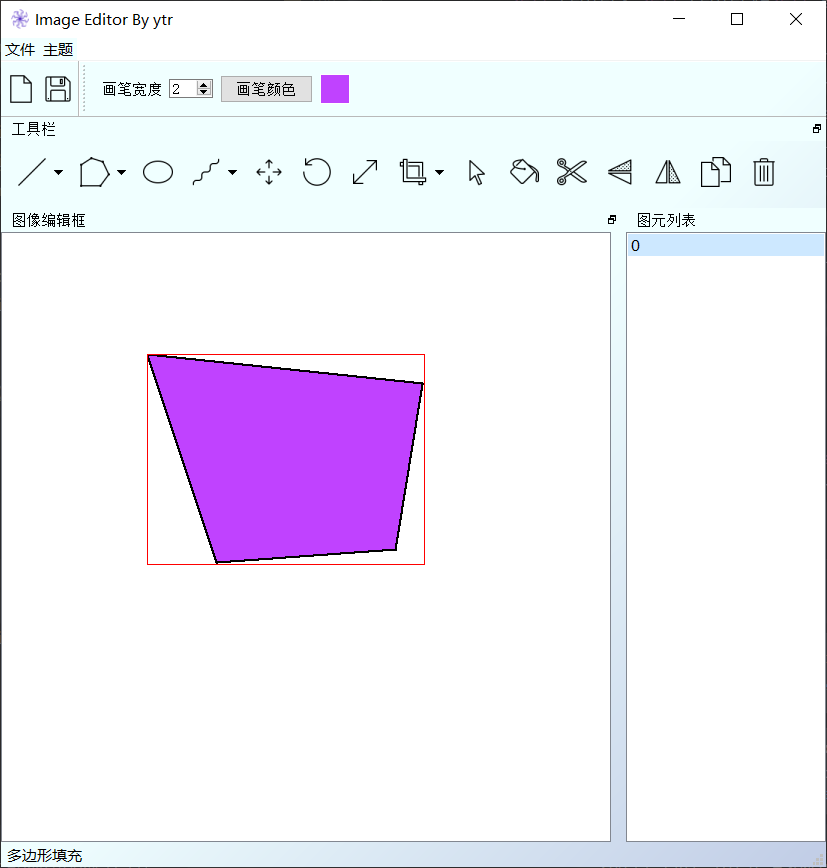
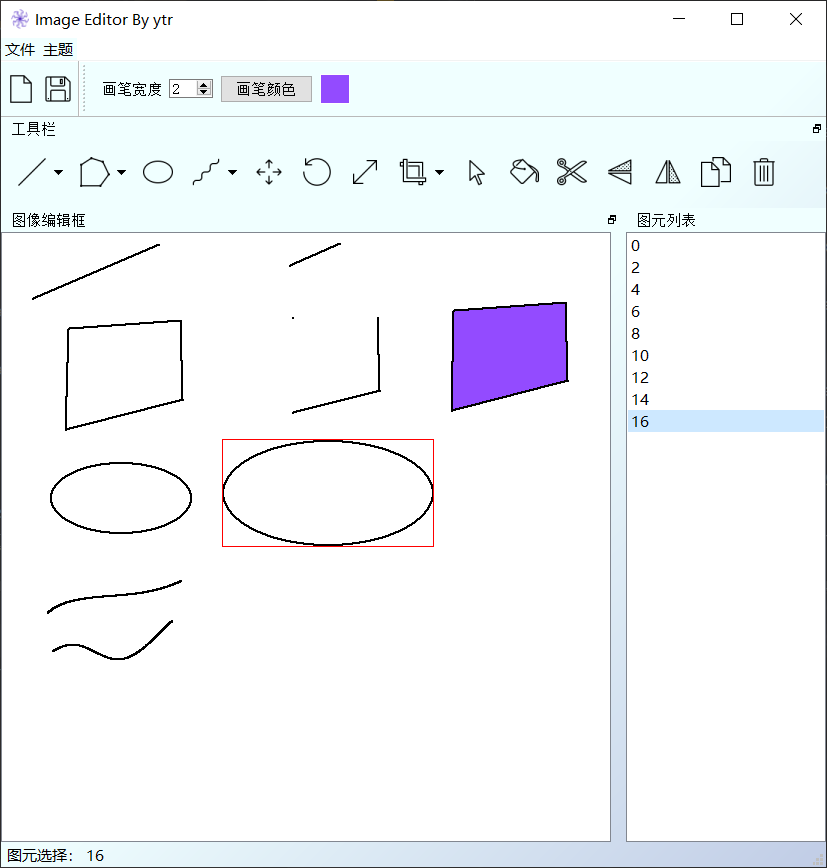
本实验主要为了实现一个图形绘制系统,主要内容包括了底层算法实现,命令行系统完善和图形界面系 统(pyqt)的实现;
 根据大实验的具体要求,主要通过Python3完成了以下模块的内容: 核心算法模块:cg algorithm.py(除Liang-Barsky完成)
根据大实验的具体要求,主要通过Python3完成了以下模块的内容: 核心算法模块:cg algorithm.py(除Liang-Barsky完成)
 命令行界面程序:cg cli.py(完成)
命令行界面程序:cg cli.py(完成)
 用户交互界面(待做)
用户交互界面(待做)
算法介绍
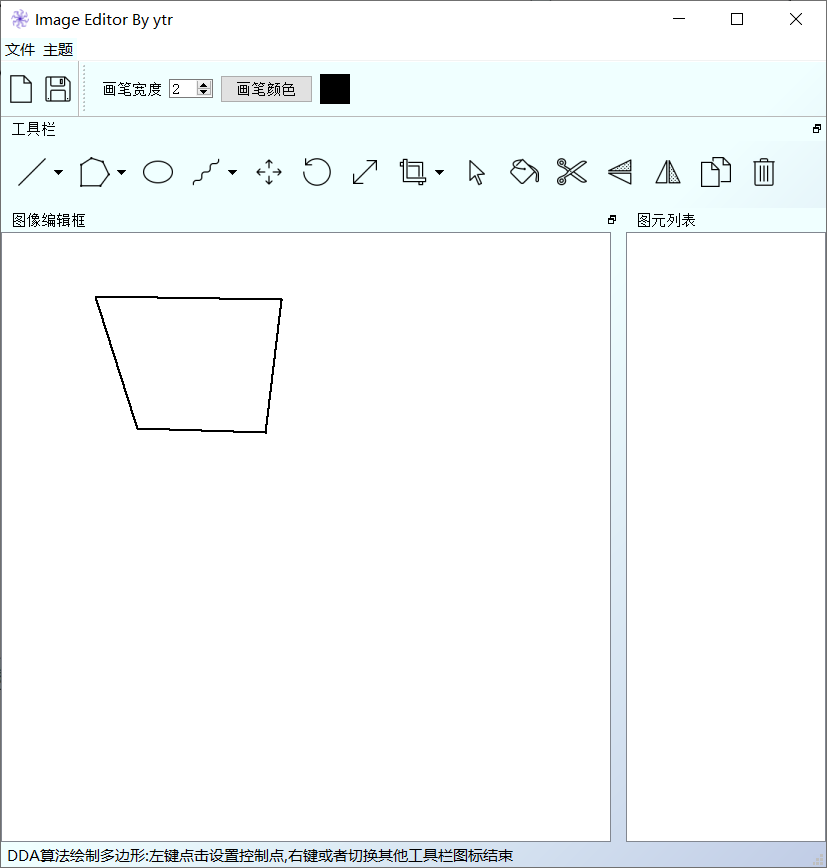
直线生成
DDA算法
DDA算法是计算机图形学基本的绘制直线算法,主要的思想来源 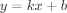 ,显然,已知两个端点
,显然,已知两个端点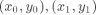 就可以知道k和b具体的值;
就可以知道k和b具体的值;
在已知k,b的情况下,只需要知道x,y中的一个就可以通过直线公式求到另一边的值;假设已知x,那么
y=kx+b;假设已知y,那么x=(1/k)*(y-b)
实际操作中绘画直线是一个迭代的过程,如果使用DDA算法,相对于前一个 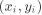 ,后一个点
,后一个点

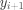
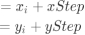
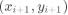 可以记作:
可以记作:

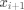
yStep,xStep即步长是通 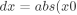
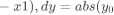 的比较确定的:
的比较确定的:

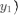

 如果dx>dy,那么说明x轴方向上面两个点的距离更远,那么设
如果dx>dy,那么说明x轴方向上面两个点的距离更远,那么设 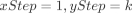 反之,说明y轴方向上面两个点的距离更远,设
反之,说明y轴方向上面两个点的距离更远,设 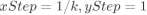

当然在具体实现上面还需要考虑斜率为正无穷的情况和斜率为0的情况,这个时候进行特判就可以实现了;