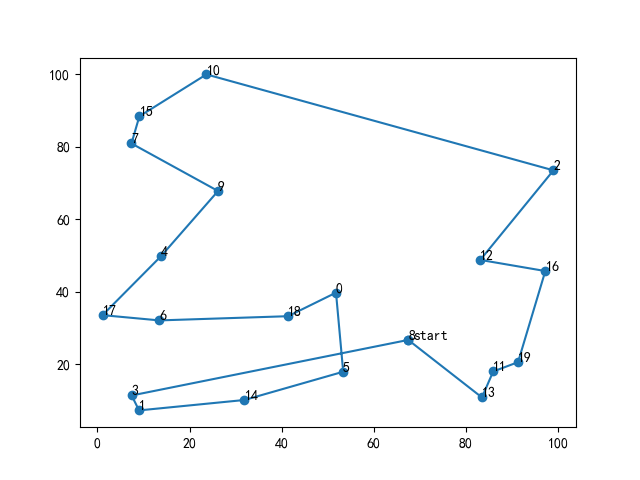
基于Python实现的遗传算法求TSP问题 课程论文+源码+使用说明
遗传算法求TSP问题
目录
一 、问题背景
1.1 遗传算法简介
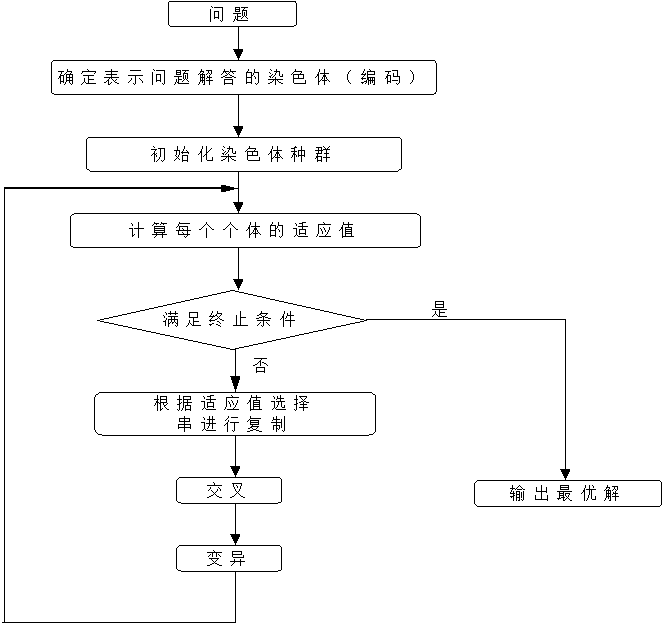
遗传算法是一种进化算法,基于自然选择和生物遗传等生物进化机制的一种搜索算法,其通过选 择、重组和变异三种操作实现优化问题的求解。它的本质是从原问题的一组解出发改进到另一组较好的 解,再从这组改进的解出发进一步改进。在搜索过程中,它利用结构和随机的信息,是满足目标的决策 获得最大的生存可能,是一种概率型算法。
遗传算法主要借用生物中“适者生存”的原则,在遗传算法中,染色体对应的是数据或数组,通常由 一维的串结构数据来表示。串上的各个位置对应一个基因座,而各个位置上所取的值对等位基因。遗传 算法处理的是基因型个体,一定数量的个体组成了群体。群体的规模就是个体的数目。不同个体对环境 的适应度不同,适应度打的个体被选择进行遗传操作产生新个体。每次选择两个染色体进行产生一组新 染色体,染色体也可能发生变异,得到下一代群体。
1.2 遗传算法基本要素
1. 参数编码:可以采用位串编码、实数编码、多参数级联编码等
2. 设定初始群体:
1. 启发 / 非启发给定一组解作为初始群体
2. 确定初始群体的规模
3. 设定适应度函数:将目标函数映射为适应度函数,可以进行尺度变换来保证非负、归一等特性
4. 设定遗传操作:
1. 选择:从当前群体选出一系列优良个体,让他们产生后代个体
2. 交叉:两个个体的基因进行交叉重组来获得新个体
3. 变异:随机变动个体串基因座上的某些基因
5. 设定控制参数:例如变异概率、交叉程度、迭代上限等