Python实现并测试K-means聚类算法 课程论文+源码及数据

实现并测试K-means聚类算法


目录
机器学习与数据挖掘第二次实验报告	
实现并测试K-means聚类算法	
一	、K-Means 简述	
四	、实验结果分析	
4.1 K-Means 迭代结果	
4.2 比较不同初始化方法和距离选择的效果	
4.3 不同聚类个数下目标函数 J 的曲线	
五	、结论	
一	、K-Means 简述
聚类（Clustering）是按照某个特定的标准将一个数据集划分成若干的簇，使得同一个簇内的样本相似    性尽可能大，不同簇之间的样本差异性尽可能大。聚类的目的在于划分数据，不关心簇对应的实际标    签，是一种常见的无监督学习方法。
常见的聚类算法包括划分式的聚类方法、基于密度的聚类方法和层次化的聚类方法，其中 K-Means
聚类是常见的划分式聚类方法。
KMeans 算法的算法效率高，聚类形状成球形，抗噪声性能较差，异常数据容易影响聚类的效果。
算法步骤 K-Means 算法的主要步骤如下：
1. 预先选择 K 个样本作为簇的中心
2. 计算每个样本到这 K 个中心的距离
3. 将每个样本分配给距离最近的簇
1. 如果分配结果较上次没有改变，到步骤 5
4. 根据簇内的样本计算均值作为新的中心
1. 回到步骤 2
5. 返回聚类结果
初始化方法 K-Means 的初始化可以采取下列三种方法：
1. 随机法：随机选择 K 个样本点作为初始中心
2. 最远距离法：随机选择一个样本点，然后从剩余样本中选择距离最远的一个样本作为中心，然 后计算已选中心的平均值，选取与该平均点距离最远的样本作为新的中心，直到选满 K 个中心。
3. 随机最远距离法：结合上述两种方法，可以是每次选取最远的若干个样本点，从中随机选取一 个中心；或者先选取若干个样本点，在从中选离已选中心最远的样本点。
距离计算 样本点距离的计算方式有多种，在实验中我们选取了欧氏距离和曼哈顿距离：



  
     
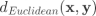
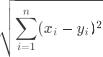
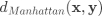
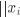
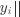
评价准则 在评价聚类效果时我们选择 NMI （标准化互信息）作为主要评价指标
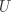
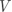
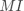
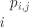
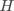
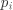设    为真实标签向量，    为预测标签向量，其中    表示两个向量之间的互信息，     表示实际标签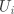为   并被预测为 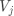 的样本占总样本的比例， 表示信息熵，  为归属于第  个簇的样本占总样本的比例。