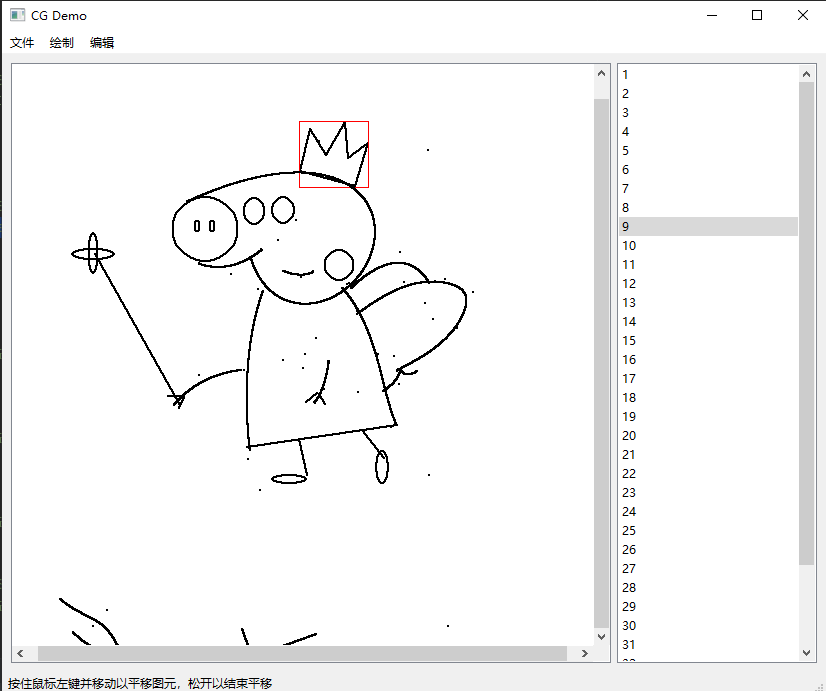
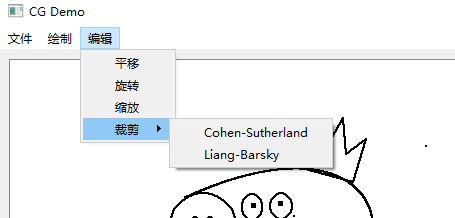
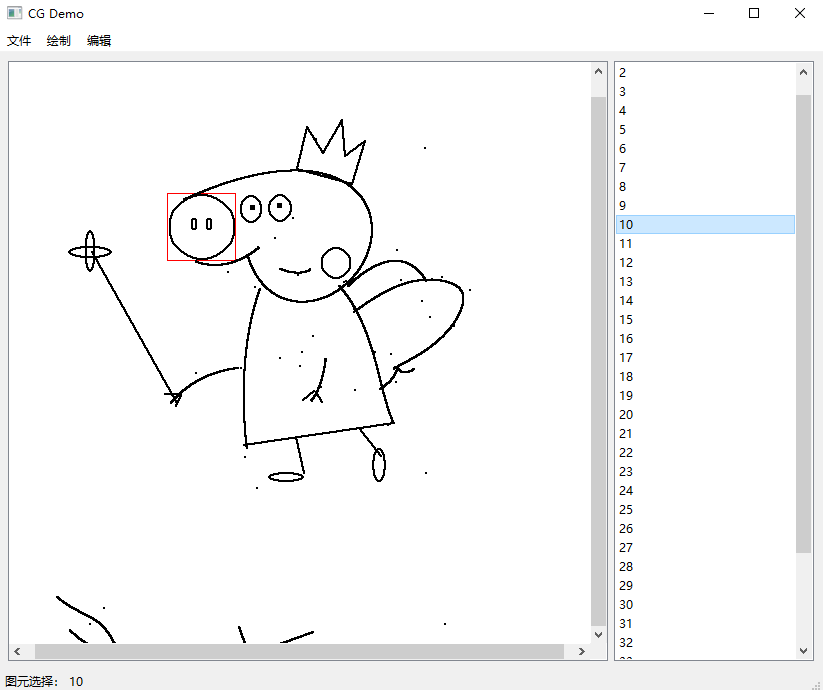
基于Python的几何图形绘图软件设计 毕业论文+项目源码+使用说明书+演示视频
目录
1 综述 2
2 算法介绍 2
2.1 绘制线段 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2.1.1 DDA 算法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2.1.2 Bresenham 算法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
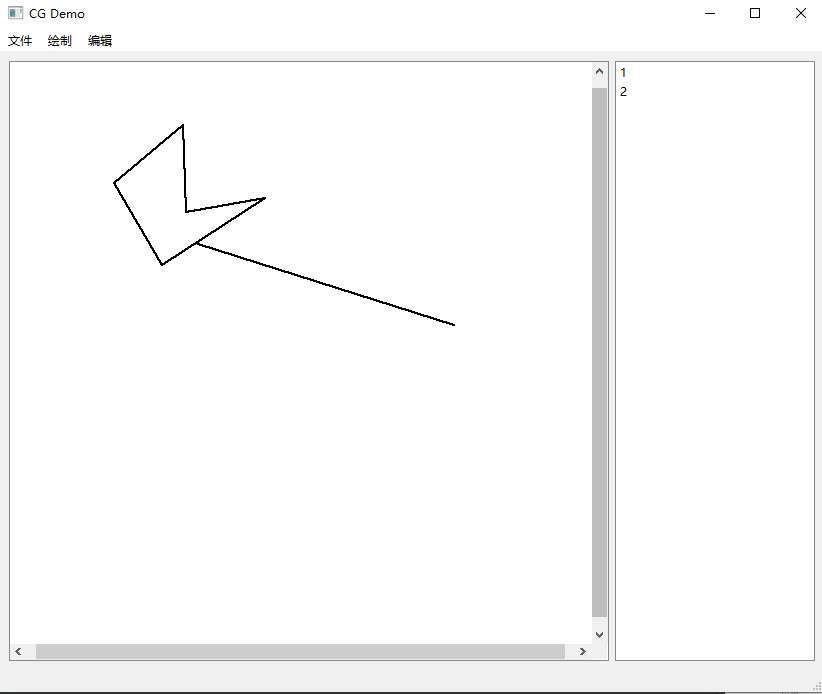
2.2 绘制多边形 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
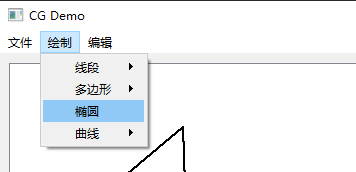
2.3 绘制椭圆 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.4 绘制曲线 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
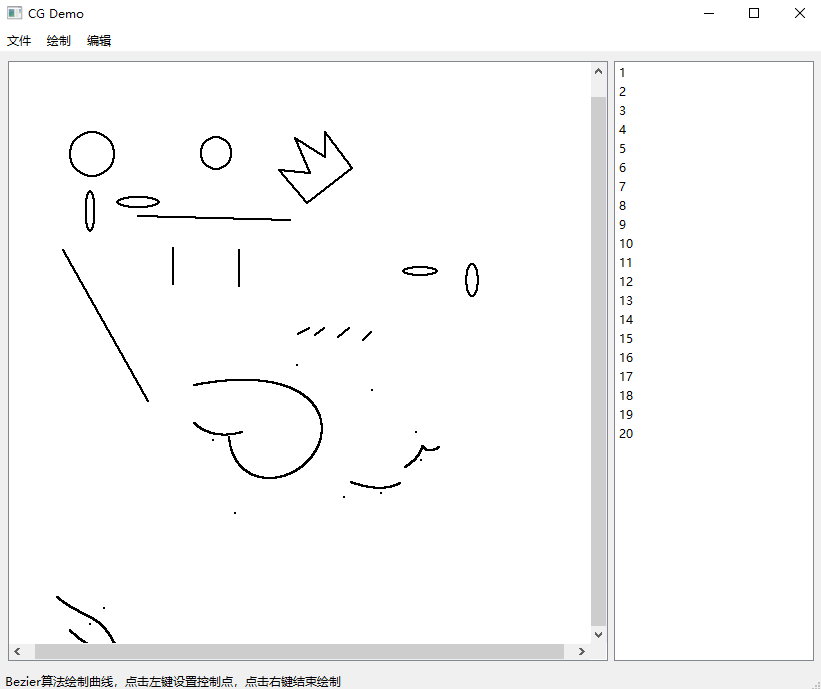
2.4.1 Bezier 曲线 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
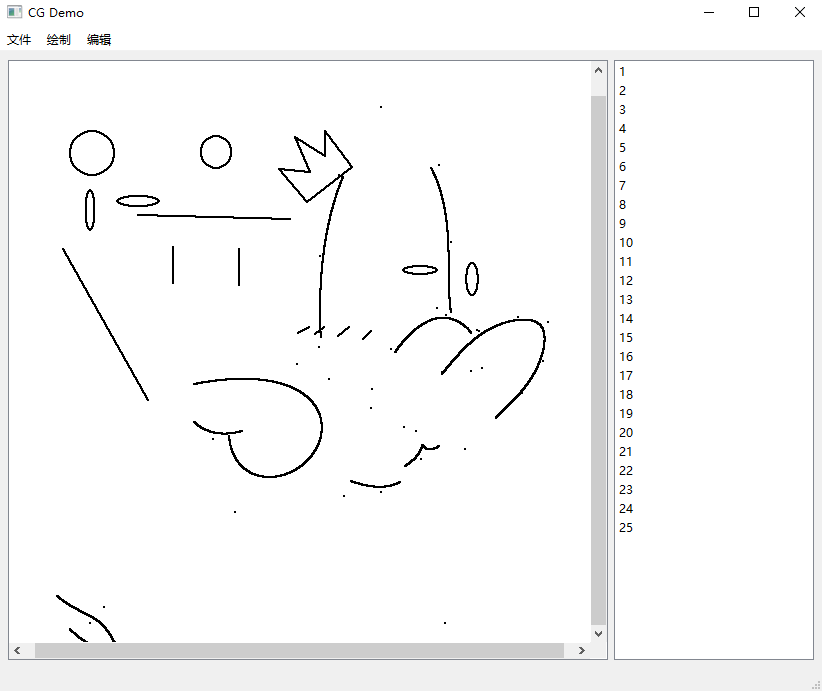
2.4.2 B 样条曲线 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.5 图元平移 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.6 图元旋转 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.7 图元缩放 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.8 裁剪线段 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.8.1 Cohen-Sutherland 裁剪算法 . . . . . . . . . . . . . . . . . . . . . . . 9
3 系统介绍 11
3.1 命令行界面 CLI 11
3.2 用户交互界面 GUI 14
3.2.1 实验环境 14
3.2.2 代码结构 14
3.2.3 实现思路 15
4 总结 17
1 综述
本实验要求跟随课程进度在项目中实现各种图形学算法,最终完成一个完整的图形学系统,进度自由安排。在 12 月,我的进度如下:
• 核心算法模块 cg_algorithm.py 已完成;
• 命令行界面(CLI)程序 cg_cli.py 已完成;
• 用户交互界面(GUI)程序 cg_gui.py 已完成;
2 算法介绍
2.1 绘制线段
2.1.1 DDA 算法
DDA 算法主要是利用了增量的思想,通过同时对 x 和 y 各增加一个小增量,计算下一步的 x 和 y 的值。由于已知线段的两个端点,因此我们很容易可以计算出直线方程 y = kx + b 中 k 和 b 的值。当线段的斜率的绝对值小于 1 时,线段在 y 方向上的增长速度小于在 x 方向上的增长速度,因此令 dx = 1,可根据下式按顺序得到与每个 x 对应的 y 值。