基于MATLAB的创意平板折叠桌的设计加工 毕业论文+源码

创意平板折叠桌的设计加工
摘	要
本文研究可折叠的桌子，通过几何关系建立折叠桌侧面直纹曲面和桌脚边缘线的方程；建立多目标优化模型确定折叠桌的设计过程中的折叠角度和钢筋位置，进而可以确定长方形平板材料的长度和折叠桌的最优设计加工参数；通过多目标优化模型可以完成客户任意设定的形状参数的创意平板折叠桌的设计.
针对问题一，以长方形平板中心为原点，y 轴沿小木条方向，z 轴指向桌底，建立空间直角坐标系，引入参数 u 表示直纹曲面上的任一点 P 还原到木板状态下到 x 轴的距离，参数 v 表示点 P 到 yoz 平面的距离，利用几何关系表示出点 P 的坐标，即得到直纹
曲面的参数方程. 进一步消去参数可得直纹曲面的方程为
d (y -	r 2 - x2 )sinq = z (d cosq + w -	r 2 - x2 ) .
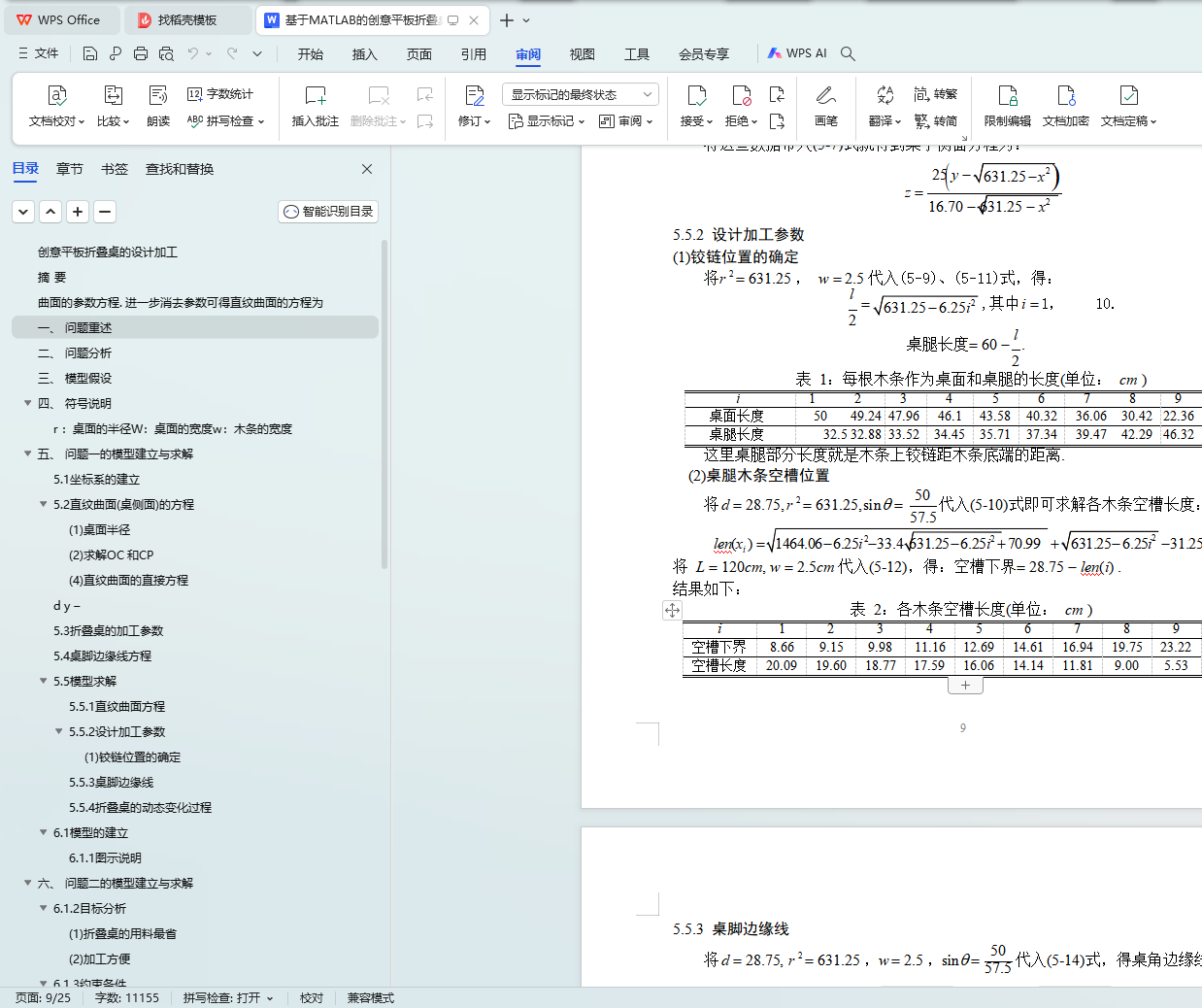
令u = L /2 ，就可得到桌脚边缘线的方程(5-12)或(5-13). 进一步可以确定设计加工参数， 如从中间到两边的木条空槽长度分别为 20.09，19.60，18.77，17.59，16.06，14.14，11.81，9.00， 5.53(cm).
针对问题二，以用料最省(板材最短)、加工方便(总开槽长度最短)为目标，各木条开槽下界不能超出木条、桌子状态下桌腿边缘不能相交、中间所有木条的桌腿不能沾地， 以及桌子的稳固性作为约束条件，建立多目标优化模型. 利用 Matlab 编程,求得最优结果为：折叠桌弯折角q 为 1.0605(弧度)，钢筋的初始位置到桌腿底端的距离s 为 43.80cm， 木板的长度 L 为 158.56cm.
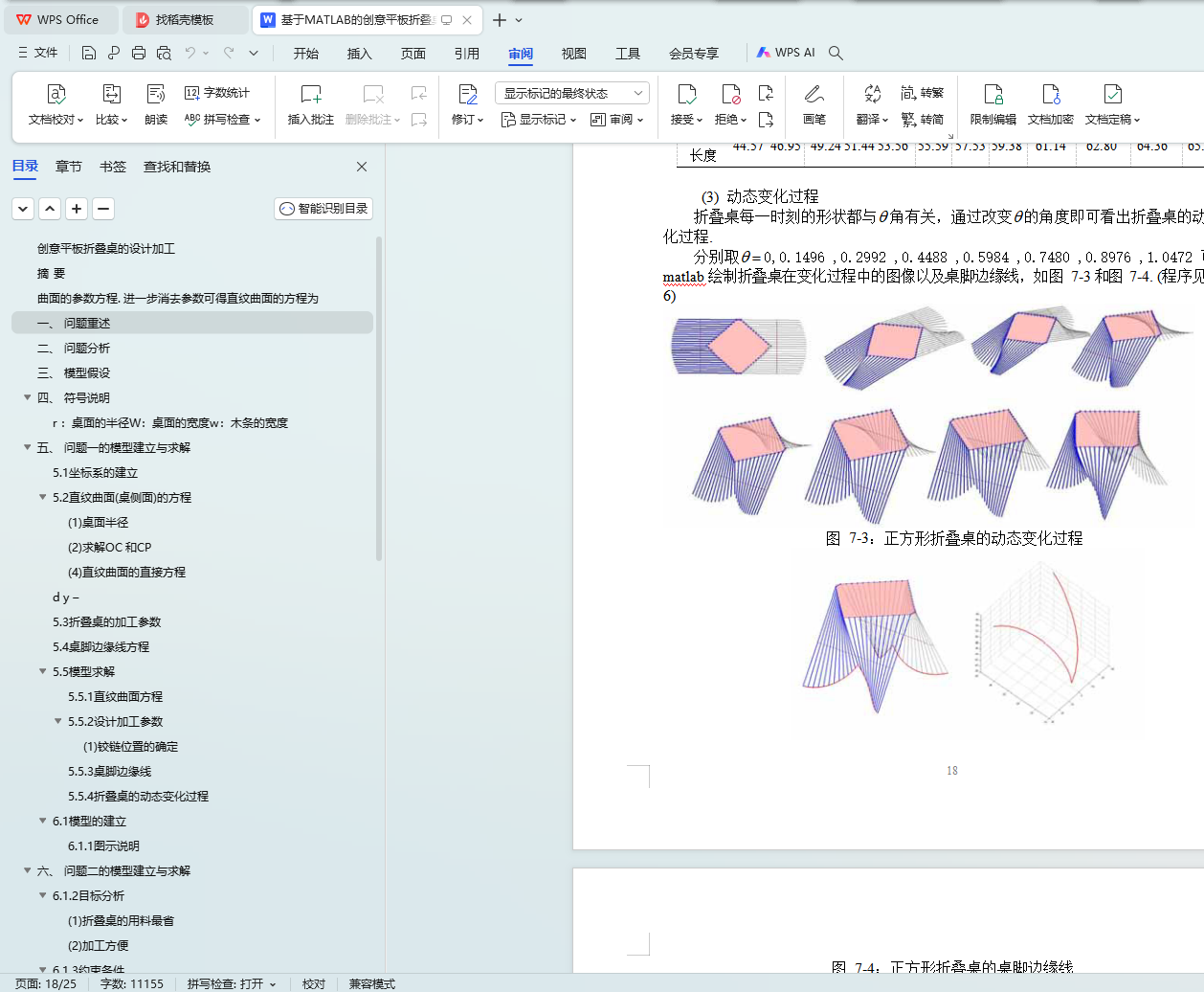
针对问题三，先将圆形折叠桌的侧面直纹曲面和桌脚边缘线的方程推广到一般形状桌面和一般形状板材，然后利用多目标优化模型设计了两种特殊形状的折叠桌：非长方形板材的正方形折叠桌和 8 字形折叠桌. 通过改变木条的旋转角度分别画出了这两种形状折叠桌的动态变化示意图，并给出了具体的设计加工参数.
关键词：直纹曲面；折叠桌；多目标优化；参数方程



目录
创意平板折叠桌的设计加工	
摘	要	
曲面的参数方程. 进一步消去参数可得直纹曲面的方程为	
一、 问题重述	
二、 问题分析	
三、 模型假设	
四、 符号说明	
r ：桌面的半径W：桌面的宽度w：木条的宽度	
五、 问题一的模型建立与求解	
5.1 坐标系的建立	
5.2 直纹曲面(桌侧面)的方程	
(1) 桌面半径	
(2) 求解OC 和CP	
(4) 直纹曲面的直接方程	
d y -	
5.3 折叠桌的加工参数	
5.4 桌脚边缘线方程	
5.5 模型求解	
5.5.1 直纹曲面方程	
5.5.2 设计加工参数	
5.5.3 桌脚边缘线	
5.5.4 折叠桌的动态变化过程	
6.1 模型的建立	
6.1.1 图示说明	
六、 问题二的模型建立与求解	
6.1.2 目标分析	
(1)折叠桌的用料最省	
(2)加工方便	
6.1.3 约束条件	
(1)空槽长度约束	
(2) 相对两桌腿不相交约束	
(3) 稳定性约束	
(4)除最边木条外的桌腿离地约束	
6.1.4 建立多目标优化模型	
i = 1, 2,・, n	
6.1.5 板材长度及空槽下界	
6.2 模型求解	
6.2.1 多目标优化模型的求解	
i = 1, 2,・, n	
6.2.2 设计加工参数的确定	
(1) 空槽长度和位置	
(2)铰链位置	
6.2.3 桌子示意图	
七、 问题三的模型建立和求解	
7.1	直纹曲面和桌脚边缘线的方程	
7. 2 多目标优化模型的建立	
i = 1, 2,・, n	
7. 3 多目标优化模型的建立	
7.3.1 正方形桌面的设计	
6.2.1 节类似，可以求解出(程序见附录 5)：	
7.3.2	8 字形桌面的设计	
8.1 模型一评价与改进	
八、 模型评价与改进	
8.2 模型二评价与改进	
8.3 模型三评价与改进	
参考文献	
附录 2：圆形折叠桌的动态变化过程图绘制程序	
附录 3：多目标规划求解程序(问题 2)	
附录 5：多目标规划求解程序(问题 3)	
附录 6：正方形折叠桌的动态变化过程绘图程序	
附录 7：8 方形折叠桌的动态变化过程绘图程序