MATLAB基于卫星无源探测的空间飞行器主动段轨道估计与误差分析 毕业论文+源码
题 目 基于卫星无源探测的空间飞行器主动段轨道估计与误差分析
摘 要：
本文针对中低轨近圆轨道卫星无源探测的空间飞行器主动段轨道进行定位估计和研究。文中针对不同的问题，建立了相应的数学模型，进行分析和求解。
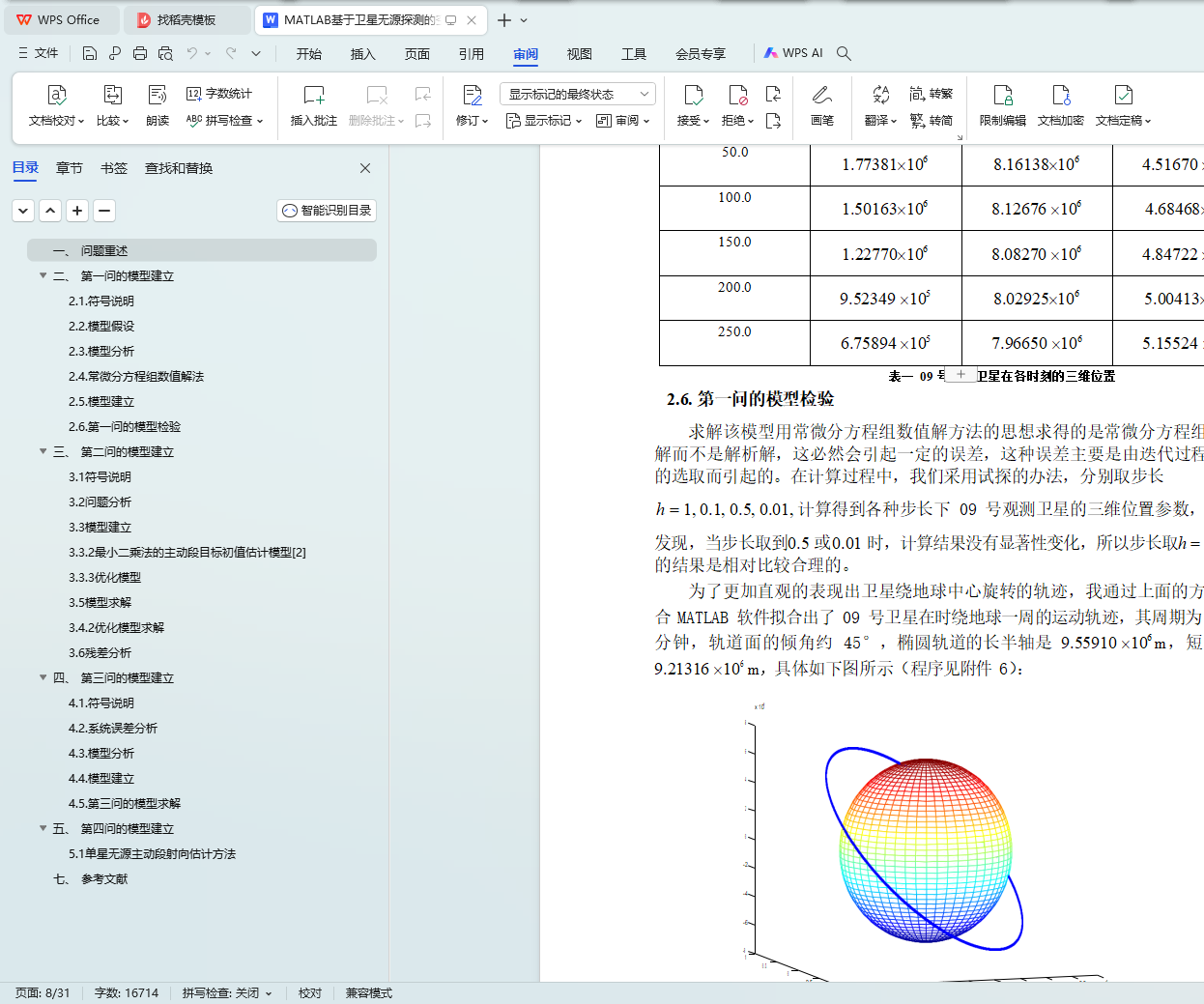
针对问题一，文中用微分方程数值解法给出了 09 号观测卫星在给定时刻的三维位置，以 50.0s 为例，该时刻下 09 号观测卫星的三维位置是（1.77381´106 ， 8.16138´106 ， 4.51670 ´106 ）。此外，还绘制了 09 号观测卫星运动轨道的图像。
针对问题二，首先通过建立几何定位模型，计算出 N 个观测点的位置参数， 并与双星插值同步后的计算结果进行比较，误差在 1.24%以内。利用待定系数法， 建立优化模型，给出了主动段目标初值估计，该法与最小二乘法给出的结果相比更直接快速。根据 12 态线性多项式拟合模型，建立状态转移矩阵，综合运用目
标跟踪算法，可演化出主动段任意时刻的速度参数，由此得到的观测点参数与几
×
何定位法除个别点外基本吻合。在m(t) 为常数的假设下，运用非线性拟合算法确定了m(t) 和vr (t) 的表达式，得m(t) = 50000.69 - 24.94t ；最后对这三个模型做残
差分析，并验证了模型结论的可信度。
针对问题三，考虑在双星同步定位的情况下，建立三轴指向误差和观测值之间的数学模型，根据同时刻观测时，双星与空间飞行器应处同一平面的约束条件， 建立优化模型，计算出dq 6 , da 6 , db 6 , dq 9 , da 9 , db 9 的值。进而参照问题二，给出结论。
针对问题四，参照运动方程的单星无源主动段射向估计方法，可利用带区间
约束的 LMF 算法，给出主动段目标轨道的初值估计。
关键词：几何定位算法 优化模型 最小二乘法 目标跟踪算法 Kalman 滤波
目录
