题 目	空间飞行器轨道估计与误差分析
摘	要：
卫星探测是当今空间飞行器观测与轨道估计的重要方式。论文针对空间飞行器轨道估计及卫星无源探测的误差分析的问题，通过使用样条插值或拟合的方法对有误差的数据进行光滑处理，然后基于交汇的思想建立了运动方程参数模型， 采用最小二乘法估计参数，得到了空间飞行器的轨道估计，并使用 LMF 法进行了系统误差分析。
对于问题一，利用卫星的初始位置和速度以及简化运动模型，将问题转化为常微分方程组的初值问题，采用 4 阶龙格库塔积分求解得到结果。
对于问题二，利用逐点交汇的思路，将 0 号空间飞行器在 06、09 号卫星观测坐标系下的坐标转换到基准坐标系下，由于误差的存在，转换后的点并不交汇， 于是通过最小二乘法求解飞行器在惯性系下的近似交汇位置。随后使用差分法求解飞行器在惯性系下的速度和加速度。在差分过程中，由于从观测量所得的飞行器位置信息含有随机误差，所以通过拟合的方法将其中的随机误差进行消除，防




止随机误差对差分的影响。
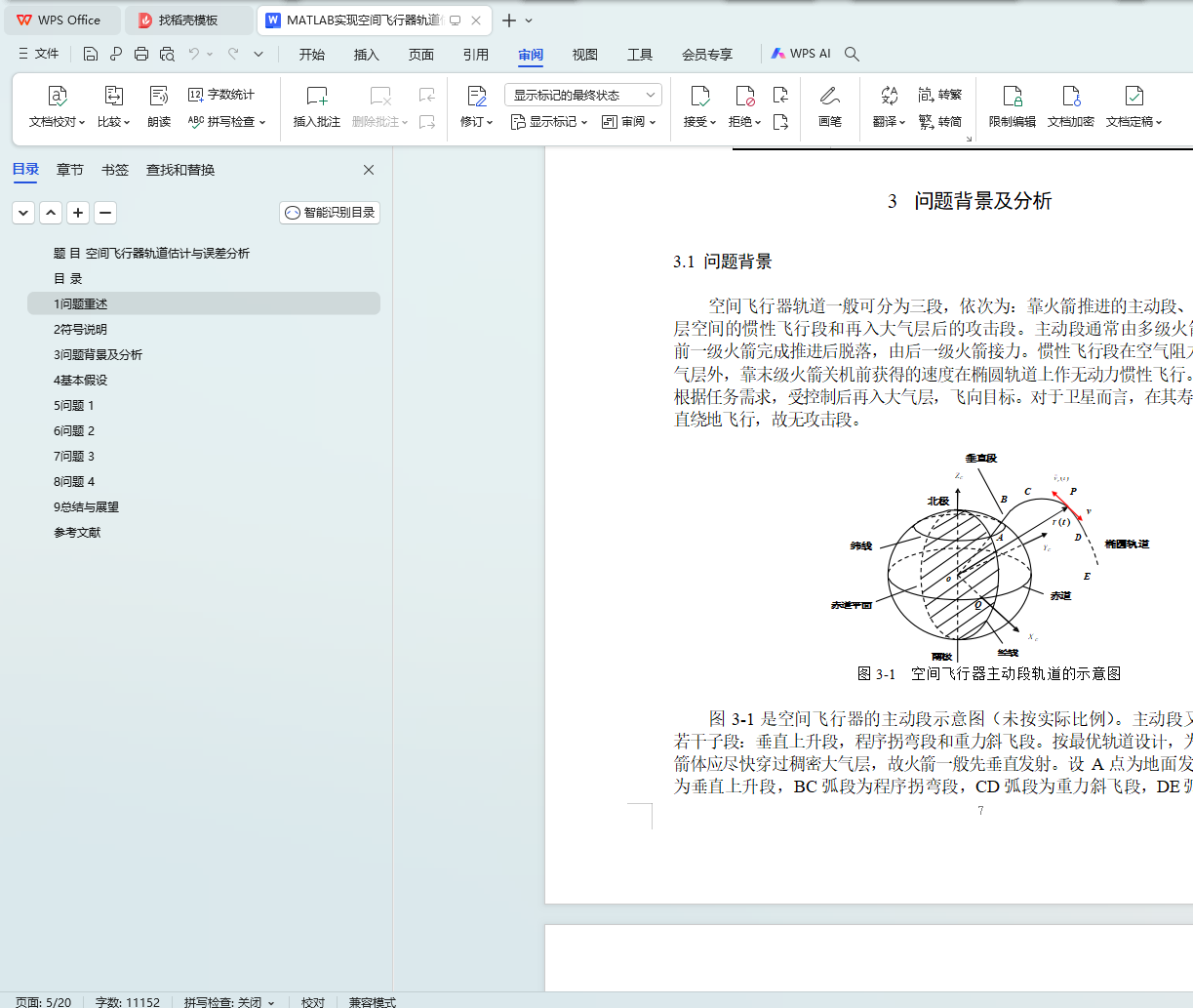
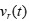为建立合理的空间飞行器运动方程，根据相关文献，设 r	大小恒定，方向
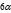
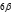
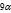与v(t) 相反；m(t) 设为一次线性函数，质量变化率为固定值。将所求的飞行器位置点带入其运动方程得到矛盾方程组，使用最小二乘法对模型参数进行估计，得到飞行器轨道估计，相关结果符合相关文献中的记录。最后由估计值与观测值计




算得残差 ：
e	= 0.9295´10-3
， e	= 0.5001´10-3
； e	=1.0696´10-3 ，




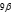e	= 0.2776´10-3 。
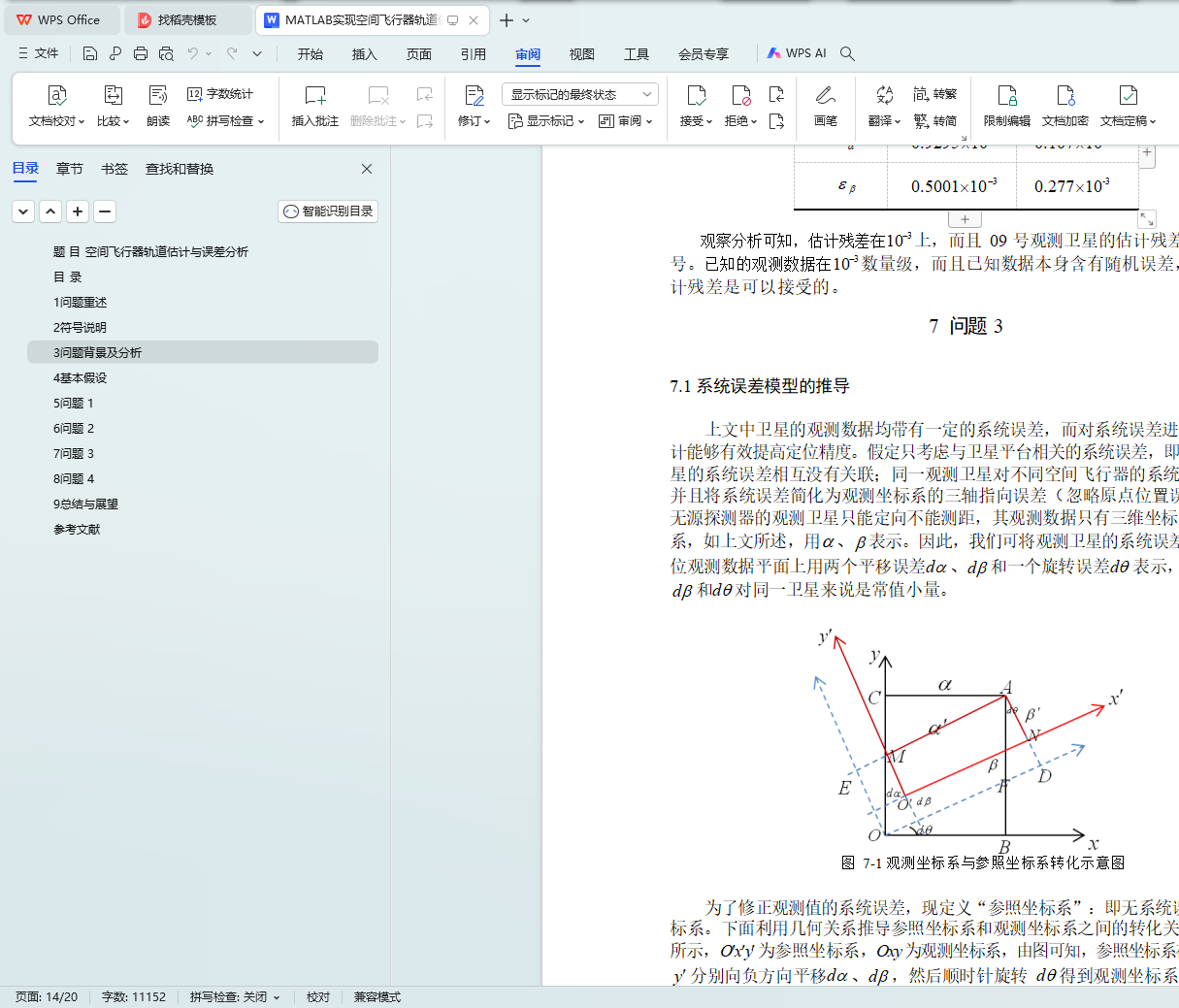
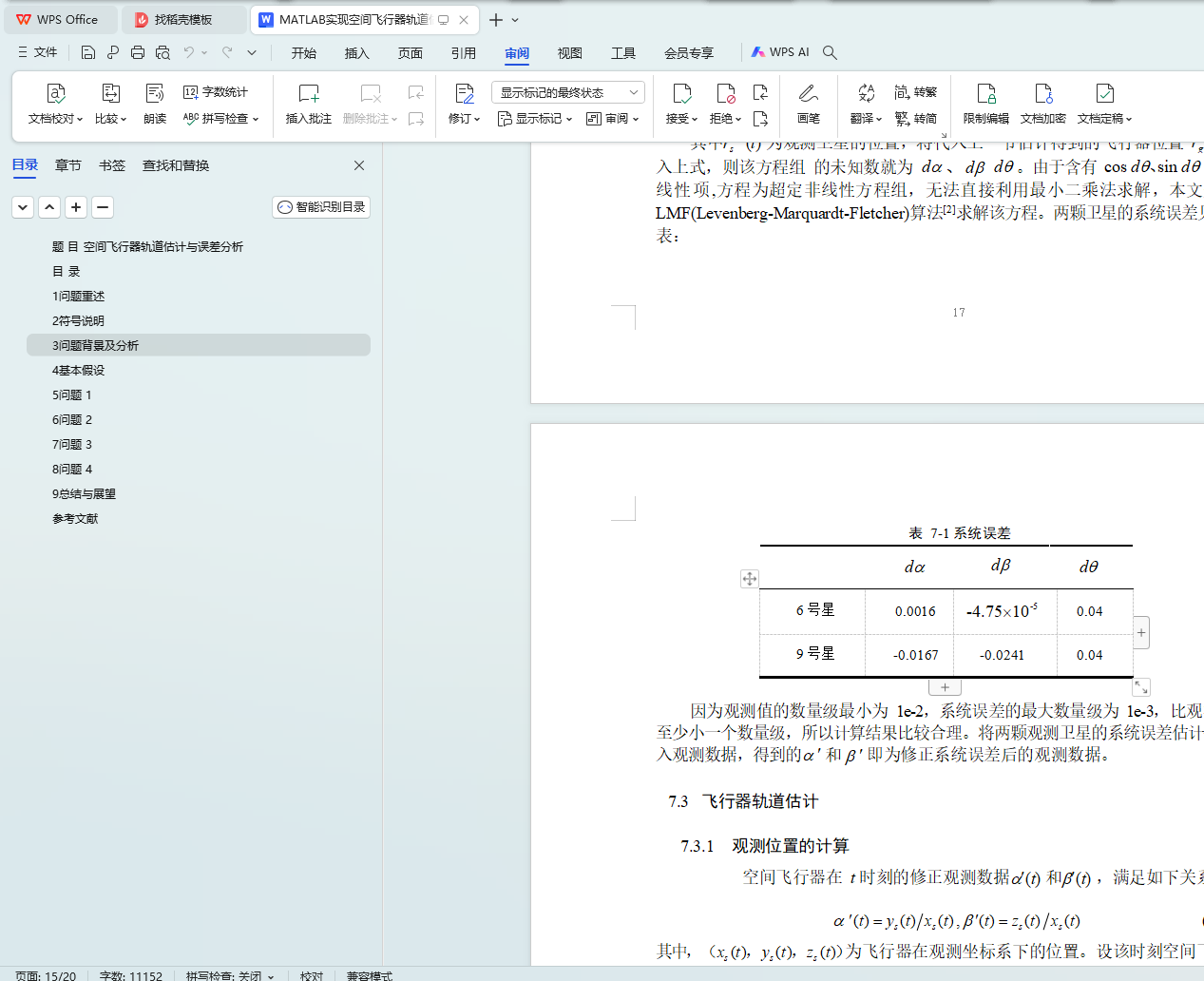
对于问题三，由于三轴指向误差表现为二维观测数据平面上的两个平移误差和一个旋转误差，分别设为da 、db 和dq 。将这些误差量叠加到观测量a 、b
后再根据卫星同步观测逐点交汇的思路，利用 LMF 方法求解超定非线性方程组， 得da = 0.0016， db =-4.75´10-5 ， dq = 0.0395； da = -0.0167， d b = -0.0241， dq9 = 0.04。
对于问题四，对于单星观测的情况，通过添加约束和先验信息，可以得到大致的轨道估计。一方面，认为飞行器轨道上的点共面且均在过地心的平面内，由此增加约束，并结合已知的运动方程进行求解。另一反面，可以通过建立飞行器轨道模版数据库与观测相对比，了解识别是何种飞行器。
本文所使用的方法有效地建立了空间飞行器的运动参数模型，得到了一定精
度的轨道估计，分析出了系统误差，但部分方法存在求解复杂，结果不稳定的缺点。
关键词：样条插值，运动方程参数模型，最小二乘法，LMF 法



目	录
1 问题重述	5
2 符号说明	6
3 问题背景及分析	6
3.1 问题背景	6
3.2 问题分析	9
4 基本假设	9
5 问题 1	9
6 问题 2	10
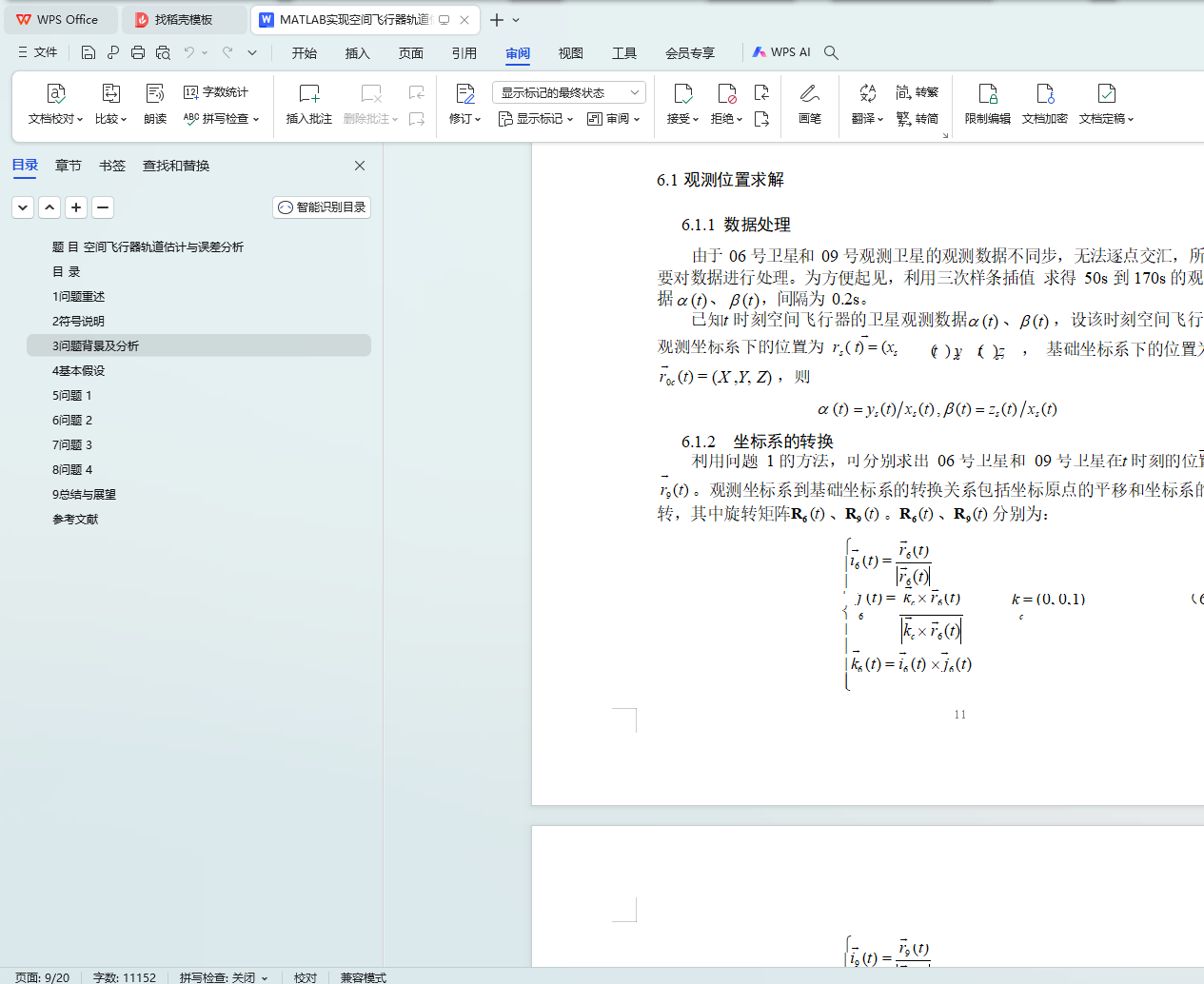
6.1 观测位置求解	10
6.1.1 数据处理	10
6.1.2 坐标系的转换	10
6.1.3 观测位置的计算	11
6.2 飞行器运动方程中参数的确定	11
6.2.1 参数确定的模型	11
6.2.2 计算方法与结果	12
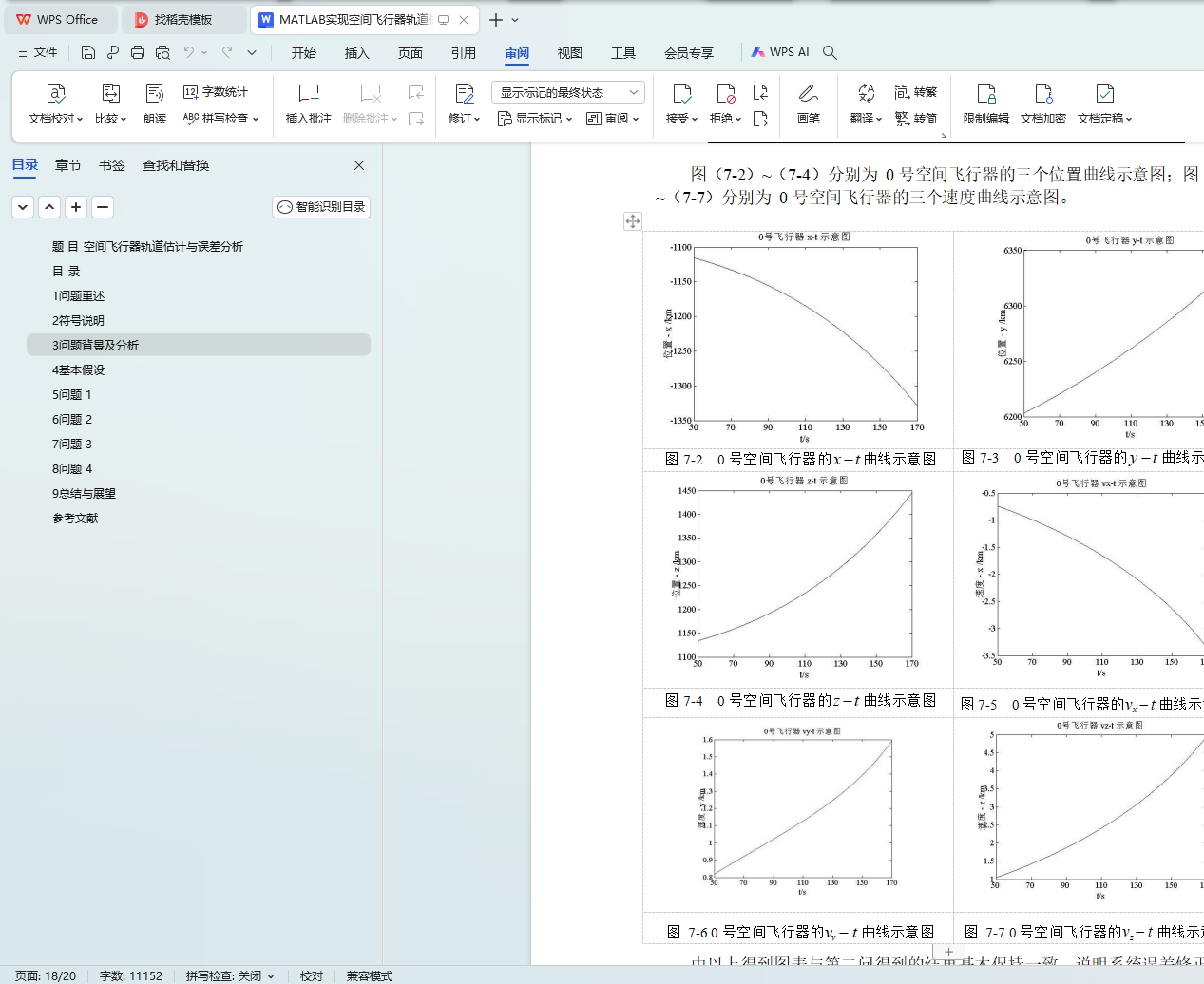
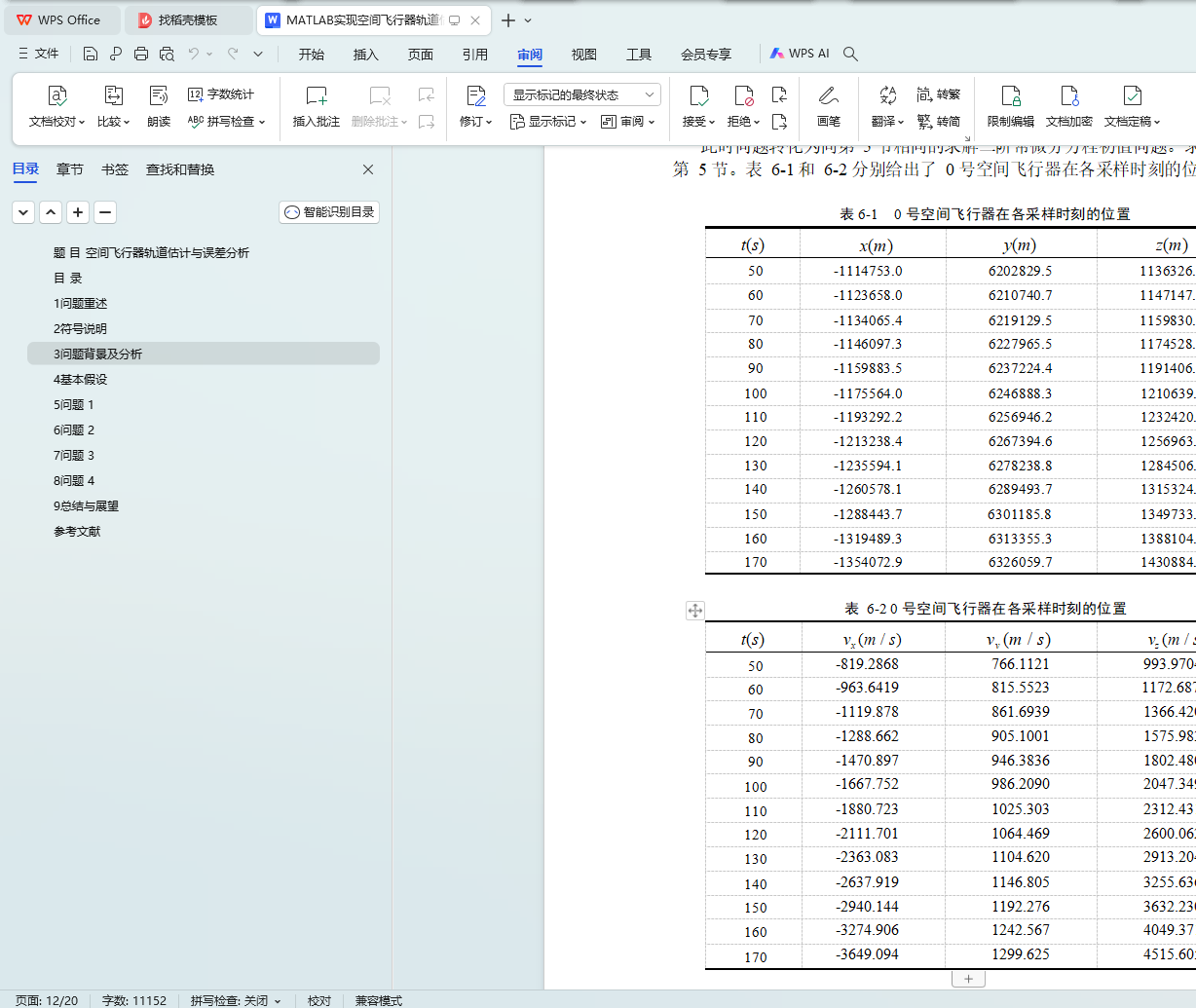
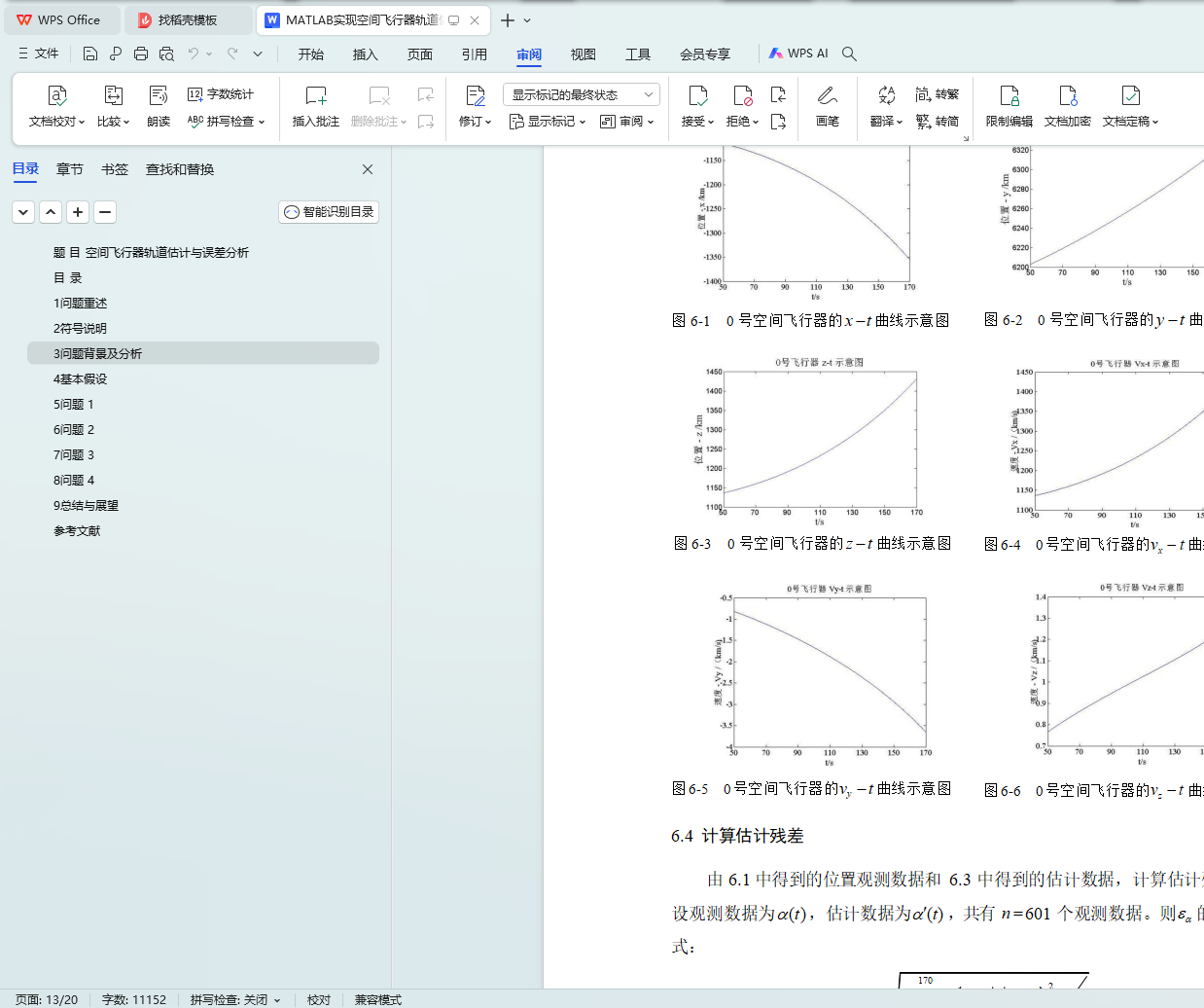
6.3 飞行器轨迹结果	13
6.4 计算估计残差	14
7 问题 3	15
7.1 系统误差模型的证明	15
7.2 系统误差估计	16
7.3 飞行器轨道估计	17
7.3.1 观测位置的计算	17
7.3.2 运动方程的确定	17
7.3.3 飞行器轨迹结果	18
7.4 计算估计残差	19
8 问题 4	20
9 总结与展望	21
参考文献	21