MATLAB实现与封堵溃口有关的重物落水后运动过程的数学模型 毕业论文+源码及数据
题 目 与封堵溃口有关的重物落水后运动过程的数学模型

摘 要:
我国经常发生洪水,溃坝溃堤进而引发泥石流灾害造成国家和人民生命财产的严重损失,而物体填堵法是解决该问题的一种有效手段,本文主要解决了物体填堵法中应在何处投放重物最合适的问题。
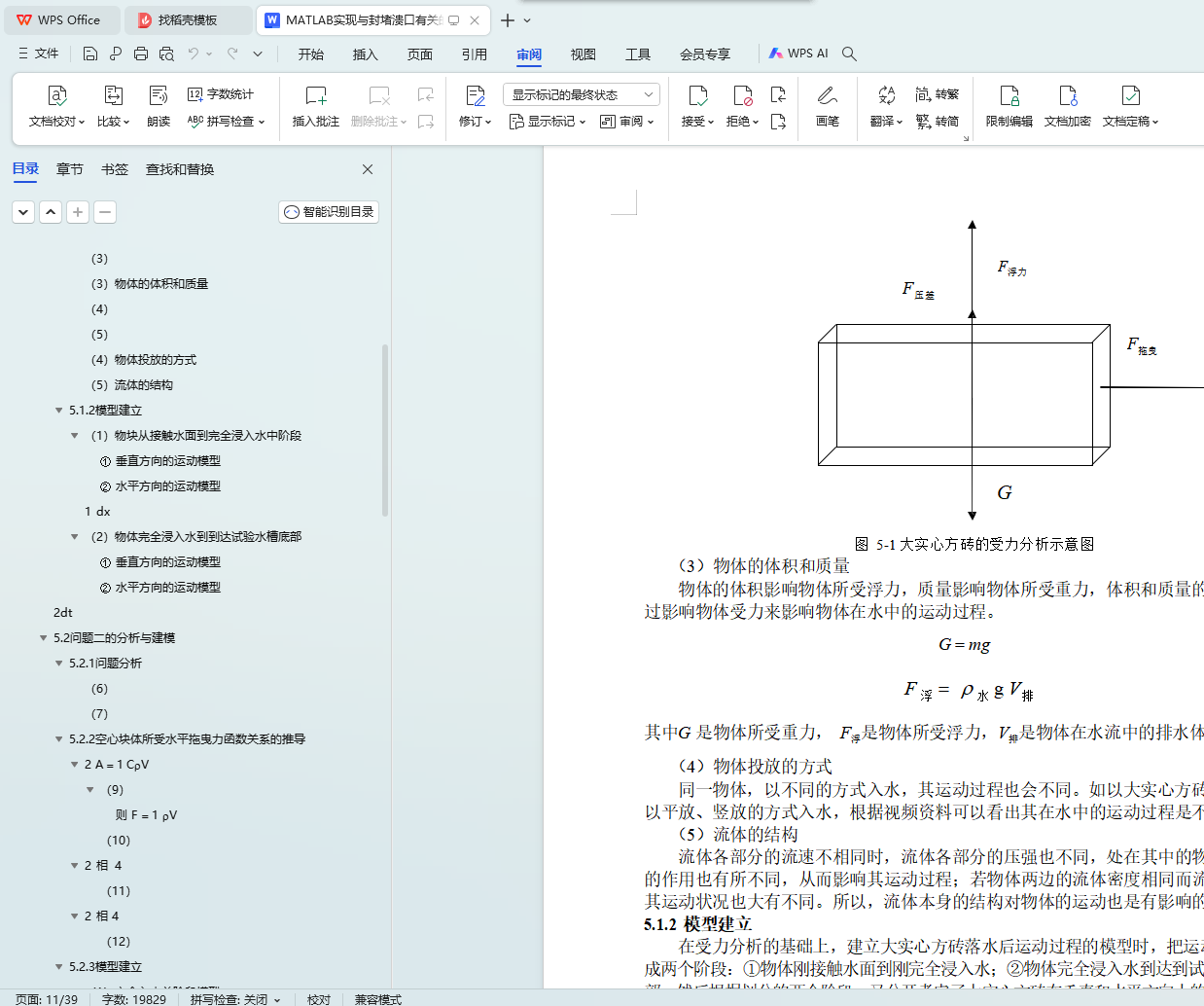
问题 1:在合理假设的前提下,通过对试验模型中各单件相关数据进行分析并参考相关资料,得出影响重物在水中运动的主要因素,包括流速、投放高度、投放方式、物体体积和重量等。然后按照物体是否完全浸入水中把运动过程分成两个阶段,再分别从垂直和水平两个运动方向考虑,建立了大实心方砖落水后运动过程的微分方程模型,详见 7~8 页。
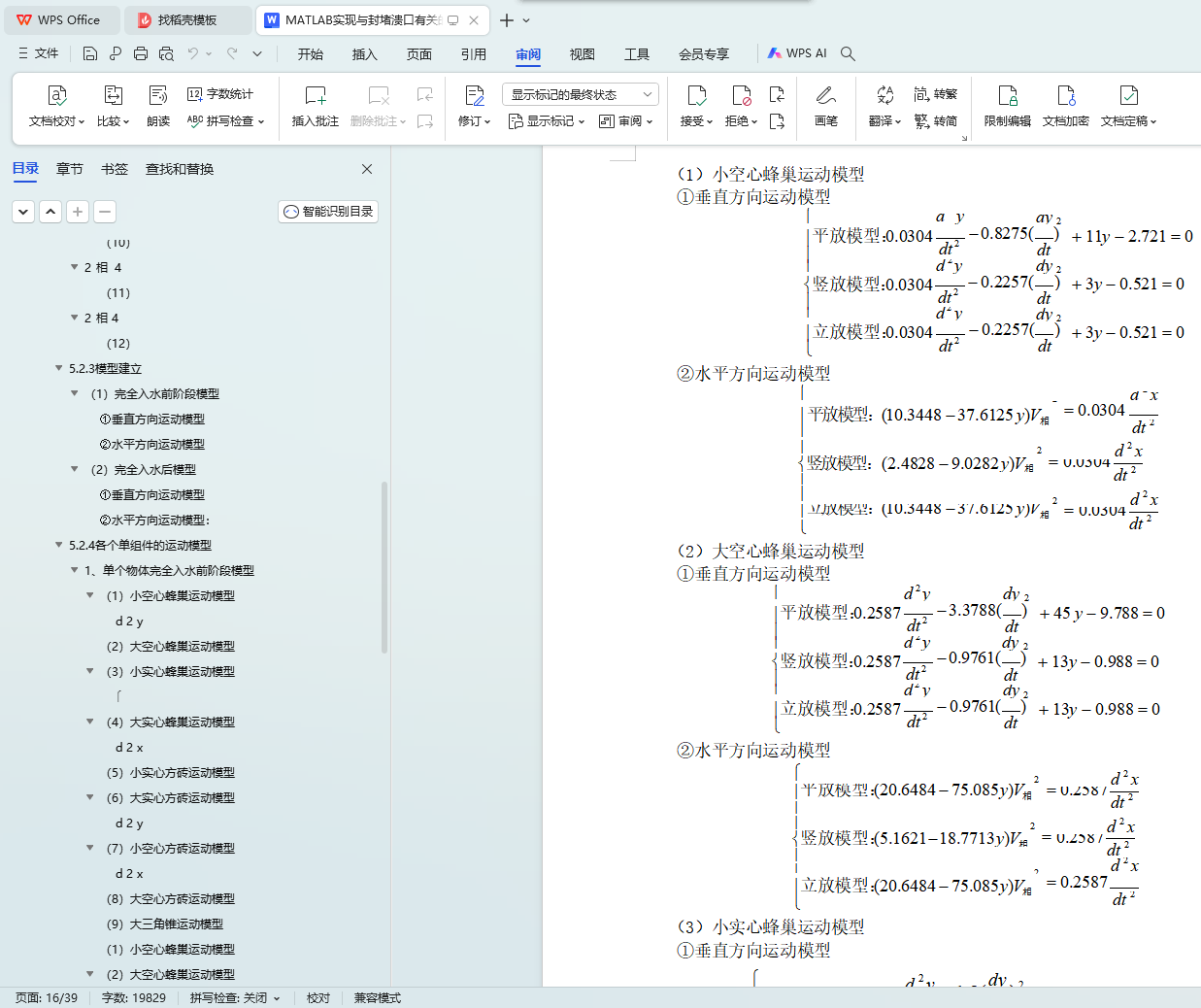
问题 2:在问题一的基础上,综合考虑各种相关因素,建立了能够适应不同情况的、描述重物水中运动过程的数学模型。在此模型的基础上,利用已知的试验数据和相关知识,分别建立了单个重物在水中运动过程的数学模型,详见 11~19 页。
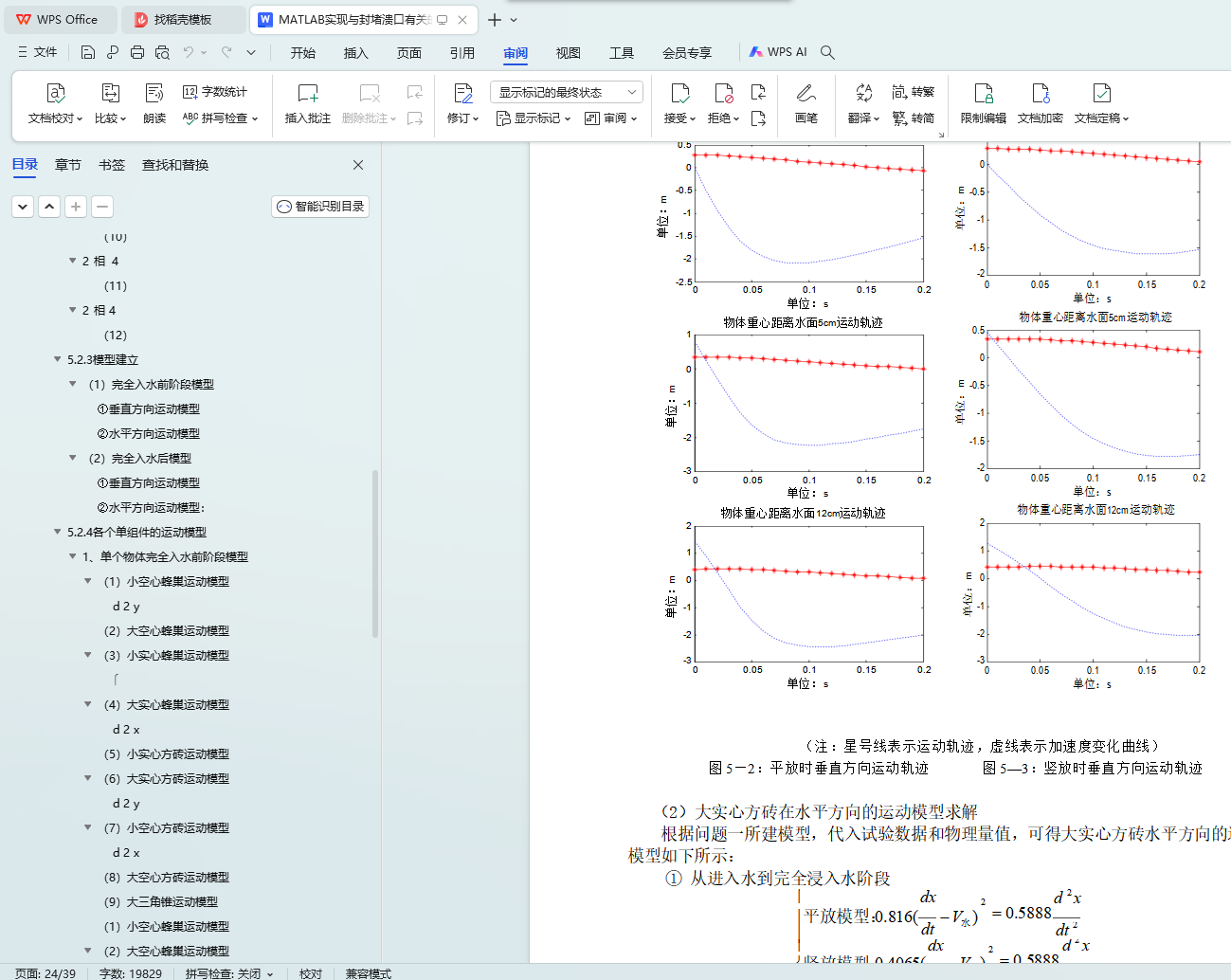
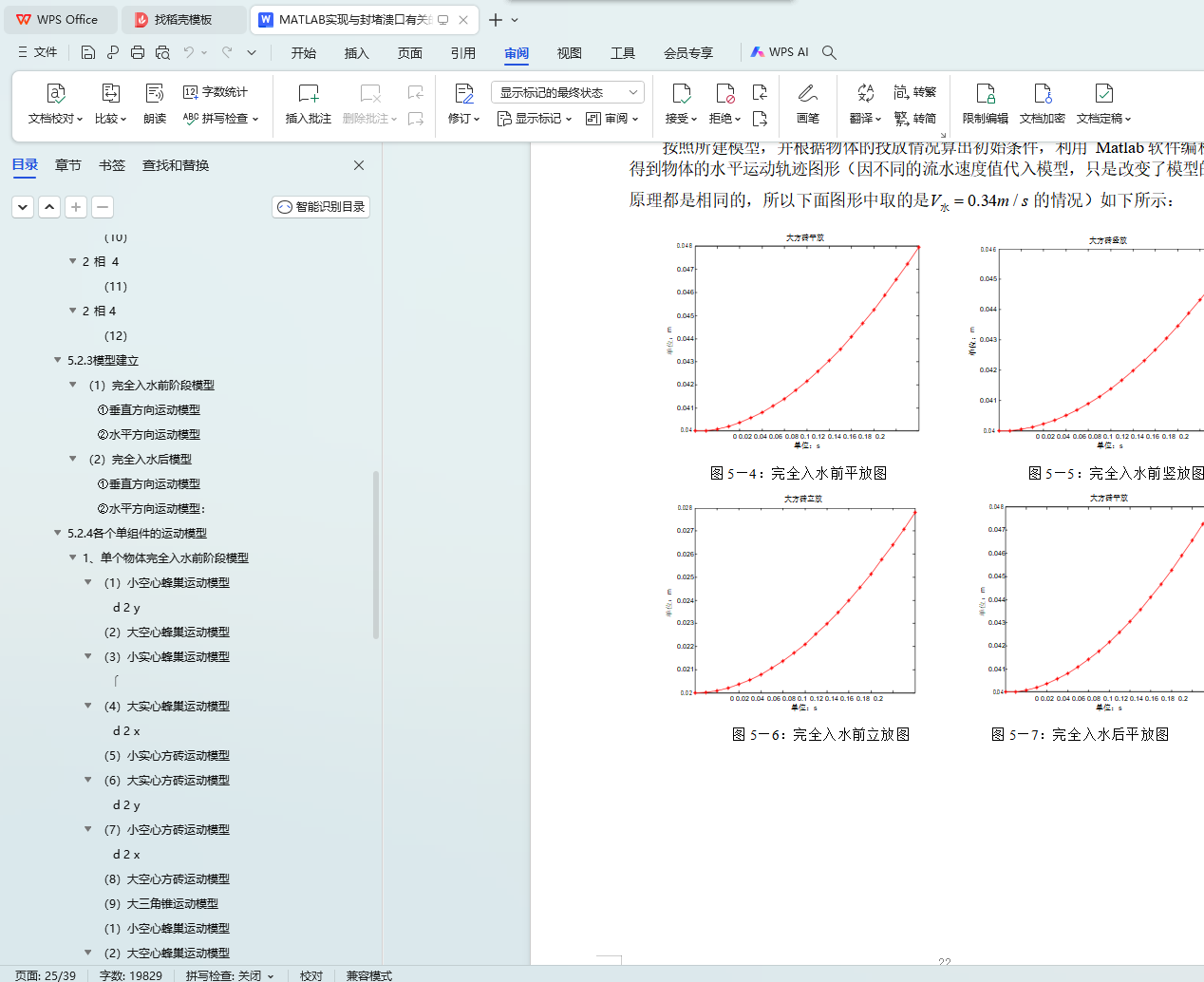
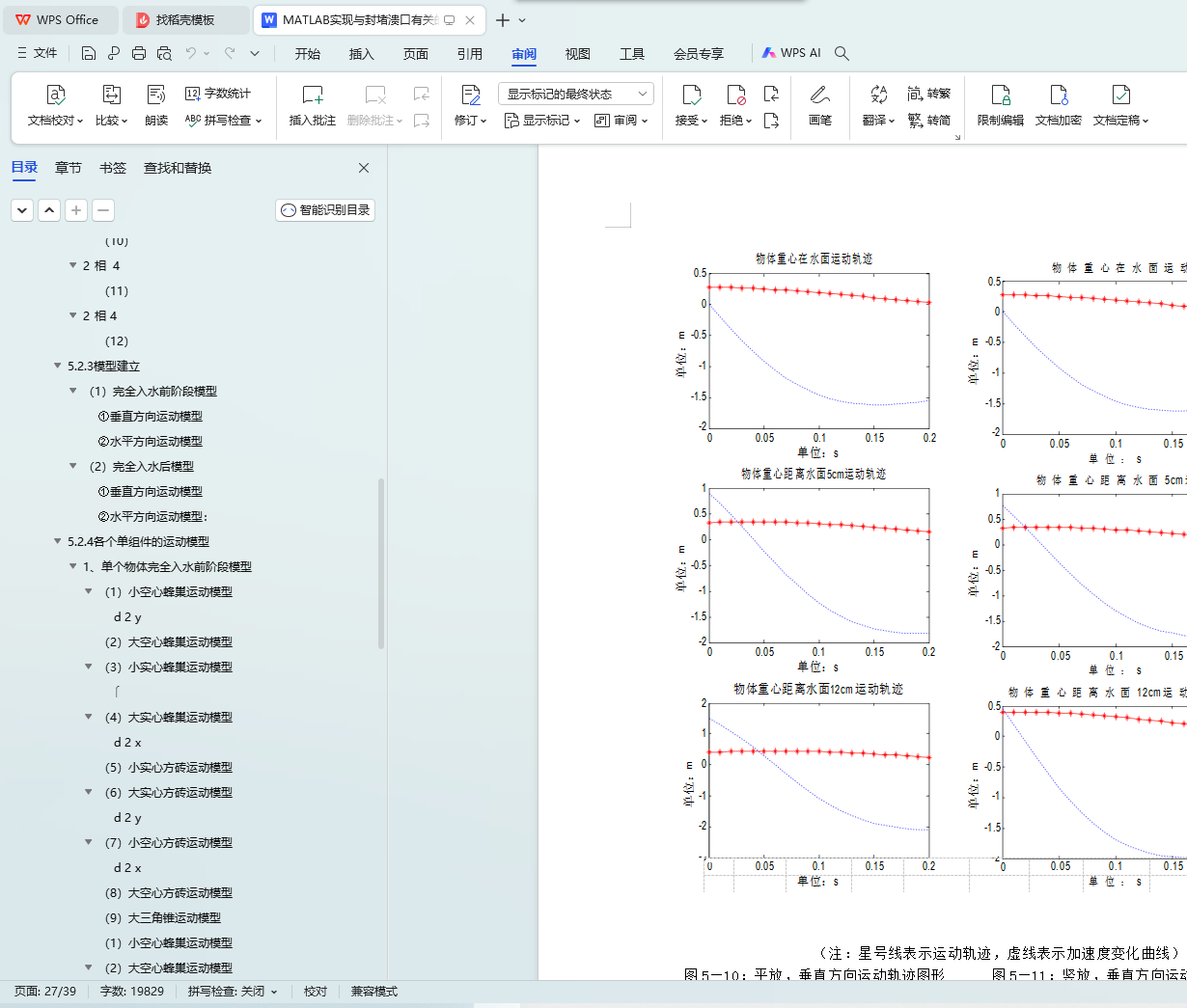
问题 3:在问题二的基础上,利用 Matlab 软件对大实心方砖和小实心方砖的运动模型求解,生成运动轨迹图形。利用光的折射原理对试验数据进行坐标值转换,然后对处理过的数据进行拟合可得到各单件的运动方程。以大实心方砖为例进行分析,对比拟合试验数据得到的和所建模型得到的运动方程,从而可以计算出离散时间点的相对误差, 其值大约为 8%~13%,符合容许条件,证明所建模型还是比较合理的。
问题 4:小型试验模型满足弗劳德准则、欧拉准则、柯西准则和韦伯准则。依据相关准则,利用几何相似和运动相似,得到所求问题与模型的速度、体积、面积等的关联式,将试验所建模型成果推广。根据补充假设条件,按照大实心方砖:长为1.0928m , 高为0.5464m ,投放高度2m ,平放情况模型(29 页)对提出的问题进行求解,如水深为3m ,水速是4m / s 时情况时,算出需提前投放距离是1.3521m ;
关键词:微分方程模型 Matlab 光折射原理 相对误差分析
与封堵溃口有关的重物落水后运动过程的数学模型
摘要
我国经常发生洪水,溃坝溃堤进而引发泥石流灾害造成国家和人民生命财产的严重损失,而物体填堵法是解决该问题的一种有效手段,本文主要解决了物体填堵法中应在何处投放重物最合适的问题。
问题 1:在合理假设的前提下,通过对试验模型中各单件相关数据进行分析并参考相关资料,得出影响重物在水中运动的主要因素,包括流速、投放高度、投放方式、物体体积和重量等。然后按照物体是否完全浸入水中把运动过程分成两个阶段,再分别从垂直和水平两个运动方向考虑,建立了大实心方砖落水后运动过程的微分方程模型,详见 7~8 页。
问题 2:在问题一的基础上,综合考虑各种相关因素,建立了能够适应不同情况的、描述重物水中运动过程的数学模型。在此模型的基础上,利用已知的试验数据和相关知识,分别建立了单个重物在水中运动过程的数学模型,详见 11~19 页。
问题 3:在问题二的基础上,利用 Matlab 软件对大实心方砖和小实心方砖的运动模型求解,生成运动轨迹图形。利用光的折射原理对试验数据进行坐标值转换,然后对处理过的数据进行拟合可得到各单件的运动方程。以大实心方砖为例进行分析,对比拟合试验数据得到的和所建模型得到的运动方程,从而可以计算出离散时间点的相对误差, 其值大约为 8%~13%,符合容许条件,证明所建模型还是比较合理的。
问题 4:小型试验模型满足弗劳德准则、欧拉准则、柯西准则和韦伯准则。依据相关准则,利用几何相似和运动相似,得到所求问题与模型的速度、体积、面积等的关联式,将试验所建模型成果推广。根据补充假设条件,按照大实心方砖:长为1.0928m , 高为0.5464m ,投放高度2m ,平放情况模型(29 页)对提出的问题进行求解,如水深为3m ,水速是4m / s 时情况时,算出需提前投放距离是1.3521m ;
关键词:微分方程模型 Matlab 光折射原理 相对误差分析
目录
1、大实心方砖垂直运动程序源代码: 平放:clc,clear